题目内容
已知抛物线y＝x2＋1，求过点P(0,0)的曲线的切线方程．
2x－y＝0或2x＋y＝0.
设抛物线过点P的切线的切点为Q (x0，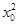
＋1)．
则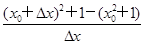
＝Δx＋2x0.
Δx→0时，Δx＋2x0→2x0.
∴
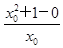＝2x0，∴x0＝1或x0＝－1.
即切点为(1,2)或(－1,2)．
所以，过P(0,0)的切线方程为y＝2x或y＝－2x.即2x－y＝0或2x＋y＝0.
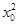＋1)．则
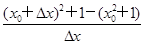＝Δx＋2x0.Δx→0时，Δx＋2x0→2x0.
∴
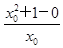＝2x0，∴x0＝1或x0＝－1.即切点为(1,2)或(－1,2)．
所以，过P(0,0)的切线方程为y＝2x或y＝－2x.即2x－y＝0或2x＋y＝0.
练习册系列答案
口算能手系列答案
相关题目
.
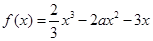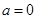时，求曲线
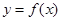在点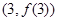
的切线方程；
,
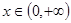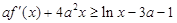恒成立,求实数
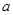的取值范围；
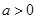时，试讨论
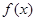在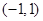
内的极值点的个数.
与
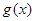是定义在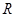
上的两个可导函数，若
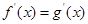,则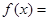
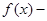
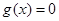
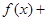
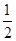x2，则f′(1)＝____．
的导函数在区间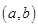
上的图像关于直线
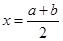对称，则函数
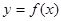在区间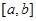
上的图象可能是（ ）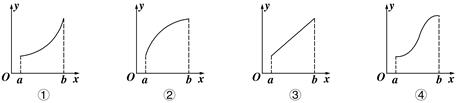
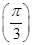等于 ( )．
