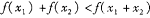题目内容
(本小题满分12分)
已知函数f(x)=a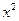 -x-lnx(a∈R).
-x-lnx(a∈R).
(Ⅰ)求函数f(x)的单调区 间;
间;
(Ⅱ)当a=1时,证明:(x-1)(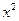 lnx-f(x))≥0.
lnx-f(x))≥0.
已知函数f(x)=a
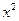 -x-lnx(a∈R).
-x-lnx(a∈R).(Ⅰ)求函数f(x)的单调区
 间;
间;(Ⅱ)当a=1时,证明:(x-1)(
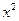 lnx-f(x))≥0.
lnx-f(x))≥0.解:(Ⅰ)函数
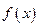 的定义域为
的定义域为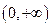 ,
,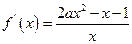
令
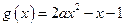 ,
,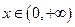
(1)当
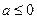 时,
时,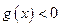 ,此时
,此时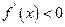 ,故
,故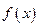 在
在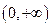 上为减函数;
上为减函数;(2)当
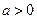 时,方程
时,方程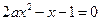 有
有 两根
两根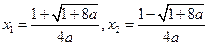 且
且 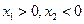 ,此时当
,此时当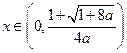 时,
时,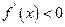 ,当
,当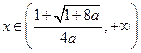 时
时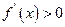 ,故
,故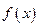 在
在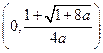 为减函数,在
为减函数,在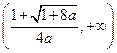 为增函数;
为增函数;所以当
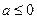 时,函数
时,函数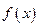 的递减区间为
的递减区间为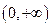 ,当
,当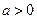 时,函数
时,函数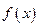 的递增区间为
的递增区间为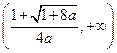 ,递减区间为
,递减区间为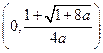 。┈┈┈┈┈6分
。┈┈┈┈┈6分(Ⅱ)当
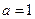 时,
时,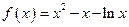 ,
,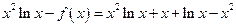 ,
,由(Ⅰ)知
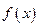 在
在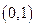 为减函数,在
为减函数,在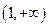 为增函数,所以
为增函数,所以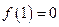 为
为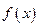 的最小值,即
的最小值,即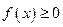 ,所以
,所以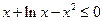 ,故当
,故当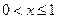 时,
时,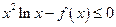 ,
,∴
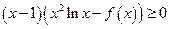 ,
, 当
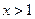 时,
时,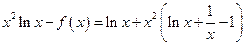 ,
,令
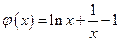 ,则
,则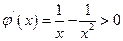 ,所以
,所以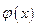 在
在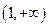 为增函数,可得出
为增函数,可得出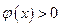 ,又因
,又因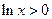 ,
,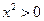 ∴
∴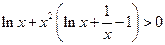 ,故当
,故当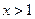 时,
时,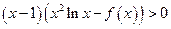 ,
,综上所述,当
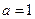 时,
时,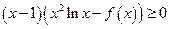 。┈┈┈┈┈12分
。┈┈┈┈┈12分略

练习册系列答案
相关题目
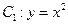 与曲线
与曲线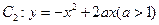 交于点O、A,直线
交于点O、A,直线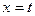 (0<t≤1)与曲线C1、C2分别相交于点D、B,连接OD、DA、AB。
(0<t≤1)与曲线C1、C2分别相交于点D、B,连接OD、DA、AB。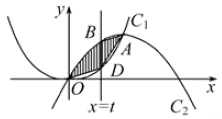
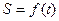 ;
;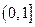 上的最大值。
上的最大值。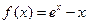 (
(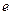 为自然对数的底数).
为自然对数的底数).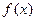 的最小值;
的最小值;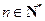 ,证明:
,证明: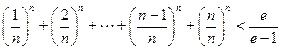 .
.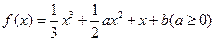 ,
,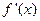 为函数
为函数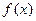 的导函数.
的导函数. 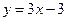 ,求
,求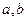 的值;
的值;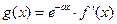 ,求函数
,求函数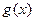 的单调区间.
的单调区间.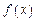 的导函数为
的导函数为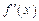 ,且
,且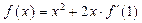 ,则
,则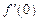 等于
等于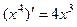 ;②
;②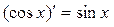 ;③
;③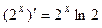 ;
;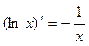 ;⑤
;⑤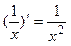 .其中正确的导数式共有( )
.其中正确的导数式共有( )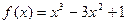 的单调减区间为
的单调减区间为 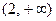
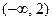
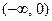
 ,宽20
,宽20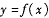 的定义域为
的定义域为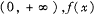 的导函数为
的导函数为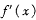 ,且对任意正数X均有
,且对任意正数X均有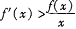 ,则下列结论中正确的是
,则下列结论中正确的是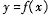 在(0,
在(0,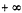 )上为增函数 B.
)上为增函数 B.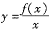 在(0,
在(0,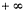 )上为减函数
)上为减函数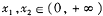 则
则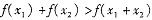
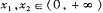 ,则
,则