题目内容
【题目】已知等差数列![]() 与数列
与数列![]() 满足
满足![]() ,
,![]() ,且
,且![]()
![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)记![]() ,
,![]() 的前n项的和分别为
的前n项的和分别为![]() ,
,![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)令![]() ,可由
,可由![]() 求出
求出![]() ,进而求出
,进而求出![]() ,得到等差数列
,得到等差数列![]() 的通项公式,于是有
的通项公式,于是有![]() ,构造数列
,构造数列![]() ,设
,设![]() ,可变形得到
,可变形得到![]() ,求出
,求出![]() ,即可得数列
,即可得数列![]() 的通项公式.其它解法参考解析;
的通项公式.其它解法参考解析;
(2)要证![]() ,即证
,即证![]() ,根据
,根据![]() 的表达式可知其关于
的表达式可知其关于![]() 单调递增,即证
单调递增,即证![]() ,再通过放缩法即可证出,多种放缩方式见解析.
,再通过放缩法即可证出,多种放缩方式见解析.
(1)令![]() 有
有![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() ,即
,即![]() .由
.由![]() 得
得![]() ,
,
设![]() ,则
,则![]() ,可得
,可得![]() ,
,
又![]() ,故
,故![]() ,则
,则![]() .
.
解法2:由![]() ,有
,有![]() ,(
,(![]() ),相减得
),相减得
![]() ,(
,(![]() ),
),
则![]() ,
,![]() ,……,
,……,![]() ,
,
相加得![]() ,则
,则![]() ,(
,(![]() ),
),
当![]() 时上式也成立.
时上式也成立.
又![]() 得
得![]() ,故
,故![]() .
.
解法3:由![]() 构造等比
构造等比![]() 也可以.
也可以.
(2)只需证![]() .
.
由(1)有![]() ,所以
,所以![]() ,记为
,记为![]() ,
,
而![]() ,所以
,所以![]() 单调递增,
单调递增,
有![]()
只需证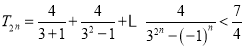 .
.
证法1:∵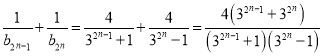
![]()
故![]()
![]() .
.
证法2:![]()
![]()
又![]()
则![]()
![]()
所以![]() .
.
证法3:∵ ,
,
∴![]()
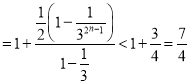 .
.

练习册系列答案
相关题目