题目内容
【题目】设数列
的前
项和为
，若对任意
，都有
，则称数列具有性质P.
（1）若数列是首项为1，公比为2的等比数列，试判断数列是否具有性质P；
（2）若正项等差数列
具有性质P，求数列的公差；
（3）已知正项数列
具有性质P，
，且对任意
，有
，求数列的通项公式.
【答案】（1）数列
不具有性质P
（2）0
（3）
【解析】
（1）根据题意写出
，
，
带入
看是否对任意
恒成立。
（2）根据题意写出，，带入对任意恒成立解出公差d即可。
（3）令m=1解出
，得到
，由等式说明数列
为以4位首项4为公比的等比数列，计算出数列的通项公式，再计算出数列
的通项公式即可。
（1）由题意知
，
，
，
，无解，
所以数列不具有性质P
（2）
为等差数列，
，
，
又因
所以
对于任意的恒成立。即
数列的公差为0
（3）令m=1得
，又为正项数列
，所以
又
所以
又
，
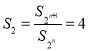
所以
练习册系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
