题目内容
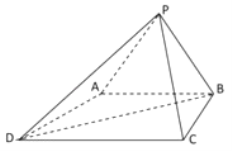
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形,![]() 平面
平面![]() ,
,![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 与平面
与平面![]() 所成角为45°,求二面角
所成角为45°,求二面角![]() 的大小.
的大小.
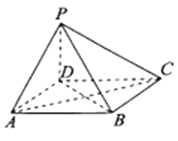
【答案】(1)证明见详解;(2)![]()
【解析】
(1)根据题意及几何关系,由线线垂直推证线面垂直即可;
(2)建立空间直角坐标系,求得两个平面的法向量,用向量法求解即可.
(1)由![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
得![]() .
.
又![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以![]() .
.
又![]() ,∴
,∴![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
故![]() 平面
平面![]() .
.
(2)由(1)可知![]() ,又
,又![]() ,
,
所以![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() 为
为![]() 在平面
在平面![]() 内的射影,
内的射影,
故![]() ,所以
,所以![]() ,
,
由(1)可知,![]() 两两垂直,
两两垂直,
如图,以![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,
![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .
.
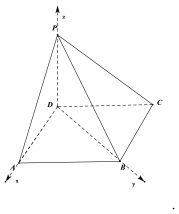
则![]()
所以![]()
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则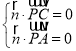 即
即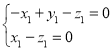 ,
,
可取![]() ,
,
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则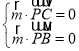 ,即
,即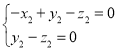 ,
,
可取![]() ,
,
故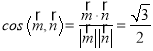
因为二面角![]() 为锐二面角,
为锐二面角,
所以二面角![]() 的大小为
的大小为![]() .
.

练习册系列答案
相关题目
【题目】随着社会发展对环保的要求,越来越多的燃油汽车被电动汽车取代,为了了解某品牌的电动汽车的节能情况,对某一辆电动汽车“行车数据”的两次记录如下表:
记录时间 | 累计里程 (单位:公里) | 平均耗电量(单位: | 剩余续航里程 (单位:公里) |
2020年1月1日 | 5000 | 0.125 | 380 |
2020年1月2日 | 5100 | 0.126 | 246 |
(注:累计里程指汽车从出厂开始累计行驶的路程,累计耗电量指汽车从出厂开始累计消耗的电量,![]()
![]() )
)
下面对该车在两次记录时间段内行驶100公里的耗电量估计正确的是( )
A.等于![]() B.
B.![]() 到
到![]() 之间C.等于
之间C.等于![]() D.大于
D.大于![]()