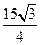题目内容
(本小题满分12分)
 某体育馆拟用运动场的边角地建一个矩形的健身室
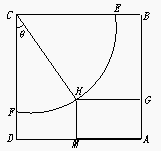
某体育馆拟用运动场的边角地建一个矩形的健身室 (如图所示),ABCD是一块边长为50 m的正方形地皮,扇形CEF是运动场的一部分,其半径为40 m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,H在 上。设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在 的何处时,该健身室的面积最大,最大面积是多少?
(如图所示),ABCD是一块边长为50 m的正方形地皮,扇形CEF是运动场的一部分,其半径为40 m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,H在 上。设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在 的何处时,该健身室的面积最大,最大面积是多少?

 某体育馆拟用运动场的边角地建一个矩形的健身室
某体育馆拟用运动场的边角地建一个矩形的健身室 (如图所示),ABCD是一块边长为50 m的正方形地皮,扇形CEF是运动场的一部分,其半径为40 m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,H在 上。设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在 的何处时,该健身室的面积最大,最大面积是多少?
(如图所示),ABCD是一块边长为50 m的正方形地皮,扇形CEF是运动场的一部分,其半径为40 m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,H在 上。设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在 的何处时,该健身室的面积最大,最大面积是多少? θ=0 或θ=
或θ=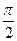
 或θ=
或θ=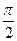
解:延长GH交CD于N,则NH="40" sinθ,CN="40" cosθ

∴HM="ND=50-40" cosθ, AM="50-40" sinθ
 …………………………2分
…………………………2分故S="(50-40" cosθ)(50-40 sinθ) …………………………3分
=100[25-20(sinθ+cosθ)+16sinθcosθ](0≤θ≤
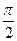 )
) …………………………4分
…………………………4分令t=sinθ+cosθ=
 sin(θ+
sin(θ+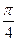 )
)
则sinθcosθ=
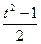 且t∈[1,
且t∈[1,  ] …………………………6分
] …………………………6分∴S=100[25-20t+8(t2-1)]=800(t-
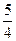 )2+450
)2+450 …………………………8分
…………………………8分又t∈[1,
 ]
] ∴当t=1时,Smax=500
∴当t=1时,Smax=500
此时
 sin(θ+
sin(θ+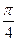 )=1
)=1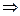 sin (θ+
sin (θ+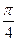 )=
)=
 …………………………10分
…………………………10分∵
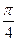 ≤θ+
≤θ+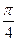 ≤
≤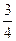 π ∴θ+
π ∴θ+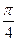 =
=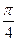 或
或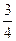 π
π
即θ=0
 或θ=
或θ=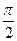
 …………………………12分
…………………………12分
练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
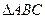 中,已知内角A、B、C成等差数列,边AC
中,已知内角A、B、C成等差数列,边AC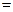 6。设内角
6。设内角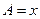 ,
, 。
。
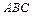 的内角
的内角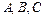 的对边分别为
的对边分别为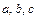 ,且
,且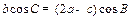 .
.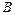 的大小;(Ⅱ)求
的大小;(Ⅱ)求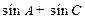 的取值范围.
的取值范围. 本题满分14分)本题共有2个小题,第1小题满分8分,第2小题满分6分.
本题满分14分)本题共有2个小题,第1小题满分8分,第2小题满分6分.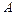 ,
,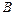 ,
,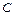 为△ABC的三个内角,向量
为△ABC的三个内角,向量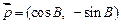 ,
,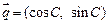 ,且
,且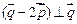 .
.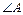 的大小;
的大小;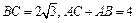 ,求△ABC的面积.
,求△ABC的面积. 中,
中,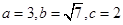 ,则角
,则角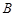 等于( )
等于( )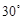
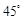
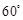
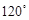
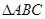 中,
中,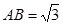 ,
,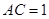 ,
,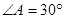 ,则
,则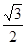
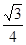
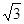
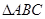 中,
中,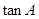 是以
是以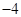 为第三项,4为第七项的等差数列的公差,
为第三项,4为第七项的等差数列的公差,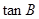 是以
是以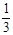 为第三项,9为第六项的等比数列的公比,则
为第三项,9为第六项的等比数列的公比,则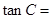 .
.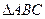 中,已知
中,已知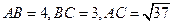 ,则
,则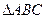 中,角A,B,C所对应的边分别是a,b,c,
中,角A,B,C所对应的边分别是a,b,c,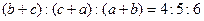 ,给出下列结论
,给出下列结论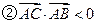
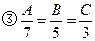 ④若b+c=8,则
④若b+c=8,则