题目内容
过点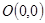 的圆C与直线
的圆C与直线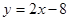 相切于点
相切于点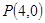 .
.
(1)求圆C的方程;
(2)已知点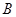 的坐标为
的坐标为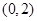 ,设
,设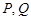 分别是直线
分别是直线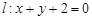 和圆
和圆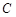 上的动点,求
上的动点,求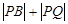 的最小值.
的最小值.
(3)在圆C上是否存在两点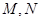 关于直线
关于直线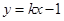 对称,且以
对称,且以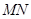 为直径的圆经过原点?若存在,写出直线
为直径的圆经过原点?若存在,写出直线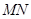 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
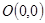 的圆C与直线
的圆C与直线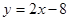 相切于点
相切于点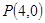 .
.(1)求圆C的方程;
(2)已知点
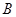 的坐标为
的坐标为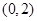 ,设
,设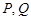 分别是直线
分别是直线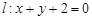 和圆
和圆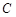 上的动点,求
上的动点,求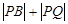 的最小值.
的最小值.(3)在圆C上是否存在两点
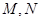 关于直线
关于直线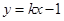 对称,且以
对称,且以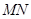 为直径的圆经过原点?若存在,写出直线
为直径的圆经过原点?若存在,写出直线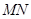 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.(1)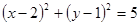
(2)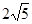
(3)直线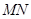 为
为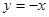 或
或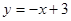
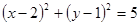
(2)
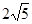
(3)直线
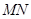 为
为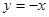 或
或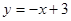
试题分析:解. (1)由已知得圆心经过点
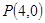 ,且与
,且与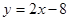 垂直的直线
垂直的直线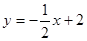 上,它又在线段OP的中垂线
上,它又在线段OP的中垂线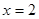 上,所以求得圆心
上,所以求得圆心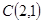 ,半径为
,半径为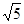 ,
,所以圆C的方程为
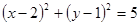 4分
4分(2)求得点
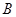
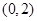 关于直线
关于直线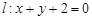 的对称点
的对称点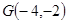 ,
,所以
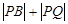
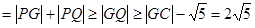 ,所以
,所以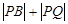 的最小值是
的最小值是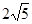 。 9分
。 9分(3)假设存在两点
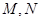 关于直线
关于直线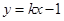 对称,则
对称,则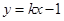 通过圆心
通过圆心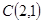 ,求得
,求得 ,所以设直线
,所以设直线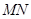 为
为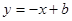 ,代入圆的方程得
,代入圆的方程得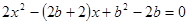 ,
,设
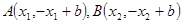 ,又
,又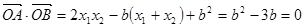 ,
,解得
 ,这时
,这时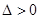 ,符合,所以存在直线
,符合,所以存在直线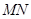 为
为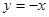 或
或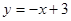 符合条件。 14分
符合条件。 14分 点评:主要是考查了直线与圆的位置关系以及直线的对称性的运用,属于中档题。

练习册系列答案
相关题目

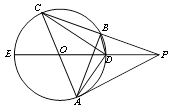
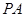 是
是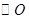 的切线,
的切线,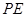 过圆心
过圆心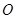 ,
, 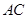 为
为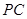 与
与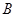 、
、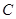 两点,连结
两点,连结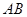 、
、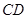 . (1) 求证:
. (1) 求证: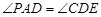 ;
;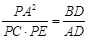 .
.
 被圆
被圆 截得的弦长为( )
截得的弦长为( )
 的切线,则切线长为( )
的切线,则切线长为( )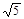
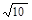
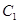 :
: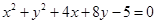 与圆
与圆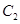 :
: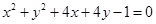 的位置关系( )
的位置关系( )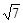 的圆的方程.
的圆的方程. 始终平分圆
始终平分圆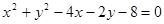 的周长,则
的周长,则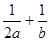 的最小值为
的最小值为