题目内容
如图,已知⊙O的半径为1,MN是⊙O的直径,过M点作⊙O的切线AM,C是AM的中点,AN交⊙O于B点,若四边形BCON是平行四边形.

(Ⅰ)求AM的长;
(Ⅱ)求sin∠ANC.

(Ⅰ)求AM的长;
(Ⅱ)求sin∠ANC.
(1)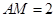 ;(2)
;(2)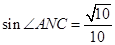 .
.
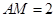 ;(2)
;(2)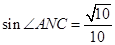 .
.试题分析:本题主要以圆为几何背景考查切线的性质以及求边长求角,可以运用平行四边形的知识证平行和相等.第一问,由于
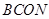 是平行四边形,所以
是平行四边形,所以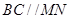 ,因为
,因为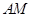 是圆
是圆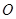 的切线,所以
的切线,所以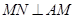 ,所以
,所以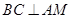 ,又因为
,又因为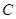 是
是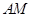 的中点,所以
的中点,所以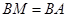 ,所以符合等腰三角形的性质;第二问,在
,所以符合等腰三角形的性质;第二问,在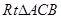 中先求
中先求 ,在
,在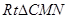 中,求
中,求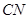 ,在
,在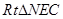 中,求
中,求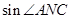 .
.试题解析:(Ⅰ)连接
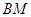 ,则
,则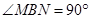 ,因为四边形
,因为四边形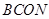 是平行四边形,所以
是平行四边形,所以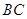 ∥
∥ ,因为
,因为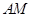 是
是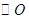 的切线,所以
的切线,所以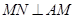 ,可得
,可得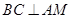 ,又因为
,又因为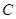 是
是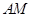 的中点,所以
的中点,所以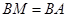 ,得
,得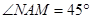 ,故
,故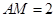 . (5分)
. (5分)(Ⅱ)作
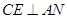 于
于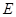 点,则
点,则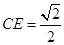 ,由(Ⅰ)可知
,由(Ⅰ)可知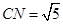 ,
,故
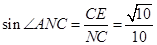 . (10分)
. (10分)
练习册系列答案
相关题目
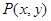 是圆
是圆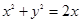 上的点
上的点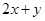 的取值范围;
的取值范围;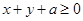 恒成立,求实数
恒成立,求实数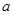 的取值范围.
的取值范围.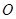 外一点
外一点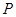 引切线与⊙
引切线与⊙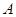 ,
,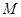 为
为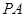 的中点,过
的中点,过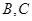 两点. 求证:
两点. 求证: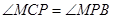
 为圆
为圆 的弦
的弦 的中点,则弦
的中点,则弦



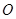 的割线
的割线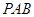 交⊙
交⊙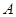 、
、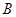 两点,割线
两点,割线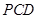 经过圆心
经过圆心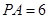 ,
,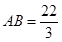 ,
,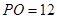 ,则⊙
,则⊙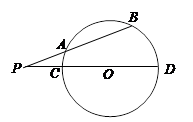
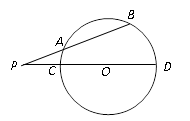
 ,那么⊙O2的半径为 .
,那么⊙O2的半径为 .
 的圆心坐标是( )
的圆心坐标是( )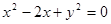 的圆心且与直线
的圆心且与直线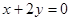 平行的直线方程是( )
平行的直线方程是( )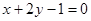
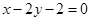


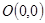 的圆C与直线
的圆C与直线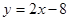 相切于点
相切于点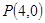 .
.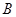 的坐标为
的坐标为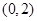 ,设
,设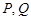 分别是直线
分别是直线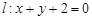 和圆
和圆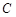 上的动点,求
上的动点,求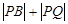 的最小值.
的最小值.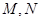 关于直线
关于直线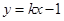 对称,且以
对称,且以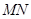 为直径的圆经过原点?若存在,写出直线
为直径的圆经过原点?若存在,写出直线