题目内容
【题目】已知M是直线l:x=﹣1上的动点,点F的坐标是(1,0),过M的直线l′与l垂直,并且l′与线段MF的垂直平分线相交于点N (Ⅰ)求点N的轨迹C的方程
(Ⅱ)设曲线C上的动点A关于x轴的对称点为A′,点P的坐标为(2,0),直线AP与曲线C的另一个交点为B(B与A′不重合),直线P′H⊥A′B,垂足为H,是否存在一个定点Q,使得|QH|为定值?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】解:(Ⅰ)由题意可知:丨NM丨=丨NF丨,即曲线C为抛物线,焦点坐标为F(1,0), 准线方程为l:x=﹣1,
∴点N的轨迹C的方程y2=4x;
(Ⅱ)设A( ![]() ,a),则A′(
,a),则A′( ![]() ,﹣a),
,﹣a),
直线AP的斜率kAP= ![]() =
= ![]() ,
,
直线AB的方程y= ![]() (x﹣2),
(x﹣2),
由 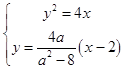 ,整理得:ay2﹣(a2﹣8)y﹣8a=0,
,整理得:ay2﹣(a2﹣8)y﹣8a=0,
设B(x2 , y2),则ay2=﹣8,则y2=﹣ ![]() ,x2=
,x2= ![]() ,
,
则B( ![]() ,﹣
,﹣ ![]() ),
),
又A′( ![]() ,﹣a),
,﹣a),
∴A′B的方程为y+a=﹣ ![]() (x﹣
(x﹣ ![]() ),
),
令y=0,则x=﹣2,
直线A′B与x轴交于定点T(﹣2,0),
△PHT为直角三角形,并且丨OP丨=丨OT丨,
∴丨OH丨= ![]() 丨TP丨=2,
丨TP丨=2,
即存在点O(0,0),使得丨OH丨为定值2,则O即为点Q(0,0).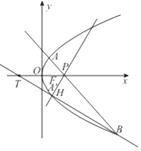
【解析】(Ⅰ)由题意可知:丨NM丨=丨NF丨,即曲线C为抛物线,焦点坐标为F(1,0),点N的轨迹C的方程y2=4x;(Ⅱ)设A( ![]() ,a),则A′(
,a),则A′( ![]() ,﹣a),直线AB的方程y=
,﹣a),直线AB的方程y= ![]() (x﹣2),代入抛物线方程,求得B的坐标,A′B的方程为y+a=﹣
(x﹣2),代入抛物线方程,求得B的坐标,A′B的方程为y+a=﹣ ![]() (x﹣
(x﹣ ![]() ),则令y=0,则x=﹣2,直线A′B与x轴交于定点T(﹣2,0),即可求得存在一个定点T(﹣2,0),使得T,A′,B三点共线,△PHT为直角三角形,并且丨OP丨=丨OT丨,丨OH丨=
),则令y=0,则x=﹣2,直线A′B与x轴交于定点T(﹣2,0),即可求得存在一个定点T(﹣2,0),使得T,A′,B三点共线,△PHT为直角三角形,并且丨OP丨=丨OT丨,丨OH丨= ![]() 丨TP丨=2,即存在点O(0,0),使得丨OH丨为定值2,则O即为点Q(0,0).
丨TP丨=2,即存在点O(0,0),使得丨OH丨为定值2,则O即为点Q(0,0).

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案