题目内容
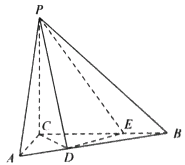
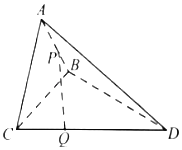
【题目】如图,在三棱锥A﹣BCD中,平面ABC⊥平面BCD,△BAC与BCD均为等腰直角三角形,且∠BAC=∠BCD=90°,BC=2,点P是线段AB上的动点,若线段CD上存在点Q,使得异面直线PQ与AC成30°的角,则线段PA长的取值范围是( )
A.(0,![]() )B.[0,
)B.[0,![]() ]C.(
]C.(![]() ,
,![]() )D.(
)D.(![]() ,
,![]() )
)
【答案】B
【解析】
由于![]() 为动点,且锥体较为规则,可考虑建系法求解,设
为动点,且锥体较为规则,可考虑建系法求解,设![]() 中点为
中点为![]() ,连接
,连接![]() ,以
,以![]() 方向为
方向为![]() 轴,
轴,![]() 方向为
方向为![]() 轴,
轴,![]() 方向为
方向为![]() 轴,结合向量夹角的余弦公式及不等关系即可求解
轴,结合向量夹角的余弦公式及不等关系即可求解
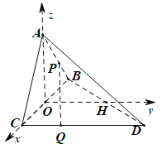
如图,由题可知,平面ABC⊥平面BCD,△BAC与BCD均为等腰直角三角形,且∠BAC=∠BCD=90°,作![]() 中点为
中点为![]() ,连接
,连接![]() ,则
,则![]() ,则
,则![]() 平面
平面![]() ,再作
,再作![]() 轴方向平行于
轴方向平行于![]() ,则
,则![]() ,故可以
,故可以![]() 为原点,建立如图所示空间直角坐标系,
为原点,建立如图所示空间直角坐标系,![]() ,设
,设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,由于
,由于![]() 与
与![]() 共线,故
共线,故![]() ,所以
,所以![]() ,
,
所以![]() ,
,
化简得![]() ,又
,又![]() ,代入化简可得:
,代入化简可得:![]() ,即
,即![]() ,所以
,所以![]() ,则
,则![]() ,即
,即
![]()
故选:B

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
【题目】空气质量AQI指数是反映空气质量状况指数,AQI指数值越小,表明空气质量越好,其对应关系如表:
AQI指数值 |
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图所示的是某市11月1日至20日AQI指数变化的折线图:
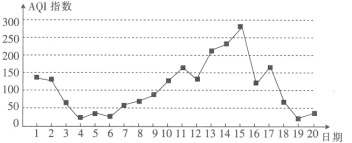
下列说法不正确的是( )
A.这![]() 天中空气质量为轻度污染的天数占
天中空气质量为轻度污染的天数占![]()
B.这![]() 天中空气质量为优和良的天数为
天中空气质量为优和良的天数为![]() 天
天
C.这![]() 天中AQI指数值的中位数略低于
天中AQI指数值的中位数略低于![]()
D.总体来说,该市11月上旬的空气质量比中旬的空气质量好