题目内容
已知各项均为正数的数列 中,
中, 是数列
是数列 的前
的前 项和,对任意
项和,对任意 ,有
,有
(Ⅰ)求常数 的值;
的值;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)设数列 的通项公式是
的通项公式是 ,前
,前 项和为
项和为 ,求证:对于任意的正整数
,求证:对于任意的正整数 ,总有
,总有 .
.
 中,
中, 是数列
是数列 的前
的前 项和,对任意
项和,对任意 ,有
,有
(Ⅰ)求常数
 的值;
的值;(Ⅱ)求数列
 的通项公式;
的通项公式;(Ⅲ)设数列
 的通项公式是
的通项公式是 ,前
,前 项和为
项和为 ,求证:对于任意的正整数
,求证:对于任意的正整数 ,总有
,总有 .
.解:(1)由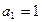 及
及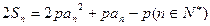 ,得:
,得:

 …………………3分
…………………3分
(2)由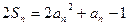 ①
①
得 ②
②
由②—①,得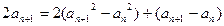
即: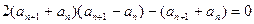
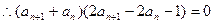 …………5分
…………5分
由于数列 各项均为正数,
各项均为正数,
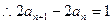 即
即  ……………………………………7分
……………………………………7分
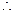 数列
数列 是首项为1,公差为
是首项为1,公差为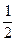 的等差数列,…………8分
的等差数列,…………8分
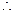 数列
数列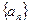 的通项公式是
的通项公式是 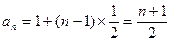 ……………9分
……………9分
(3) …………10分
…………10分
所以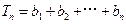
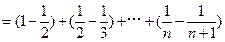

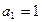 及
及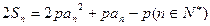 ,得:
,得:
 …………………3分
…………………3分(2)由
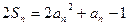 ①
①得
 ②
②由②—①,得
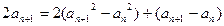
即:
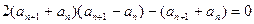
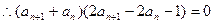 …………5分
…………5分由于数列
 各项均为正数,
各项均为正数,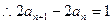 即
即  ……………………………………7分
……………………………………7分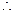 数列
数列 是首项为1,公差为
是首项为1,公差为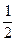 的等差数列,…………8分
的等差数列,…………8分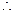 数列
数列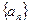 的通项公式是
的通项公式是 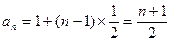 ……………9分
……………9分(3)
 …………10分
…………10分所以
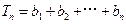
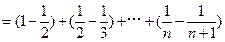

略

练习册系列答案
相关题目
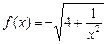 , 点
, 点 在曲线
在曲线 上
上 且
且
 为等差数列,并求数列
为等差数列,并求数列 的通
的通 项公式;
项公式; 的前n项和为
的前n项和为 ,若对于任意的
,若对于任意的 ,存在正整数t,使得
,存在正整数t,使得 恒成立,求最小正整数t的值.
恒成立,求最小正整数t的值.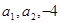 成等差数列,-1,
成等差数列,-1,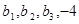 成等比数列,则
成等比数列,则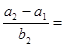 ( )
( )



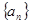 是正数等差数列,
是正数等差数列, 是正数等比数列,且a1=b1,a2n+1=b2n+1,则
是正数等比数列,且a1=b1,a2n+1=b2n+1,则 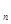 )都在直线
)都在直线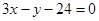 上,那么在数列{a
上,那么在数列{a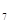 +a
+a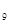 >0
>0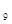 =0
=0 的前
的前 项和为
项和为 ,若
,若 ,
, ,则
,则 ( )
( )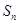 为等差数列
为等差数列 的前
的前 项和,若
项和,若 ,公差
,公差 ,
, ,则
,则  ________
________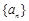 是公比为
是公比为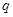 的等比数列,且
的等比数列,且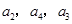 成等差数列,则
成等差数列,则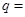 _______
_______ 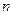 项和为
项和为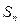 ,若
,若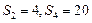 ,则该数列的公差
,则该数列的公差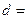 ___________
___________