题目内容
(本题满分16分)
已知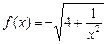 , 点
, 点 在曲线
在曲线 上
上 且
且
(Ⅰ)求证:数列 为等差数列,并求数列
为等差数列,并求数列 的通
的通 项公式;
项公式;
(Ⅱ)设数列 的前n项和为
的前n项和为 ,若对于任意的
,若对于任意的 ,存在正整数t,使得
,存在正整数t,使得 恒成立,求最小正整数t的值.
恒成立,求最小正整数t的值.
已知
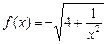 , 点
, 点 在曲线
在曲线 上
上 且
且
(Ⅰ)求证:数列
 为等差数列,并求数列
为等差数列,并求数列 的通
的通 项公式;
项公式;(Ⅱ)设数列
 的前n项和为
的前n项和为 ,若对于任意的
,若对于任意的 ,存在正整数t,使得
,存在正整数t,使得 恒成立,求最小正整数t的值.
恒成立,求最小正整数t的值.解: (Ⅰ)  ,
, …………
………… ………………………2分
………………………2分
所以 是以1为首
是以1为首 项,4为公差的等
项,4为公差的等 差数列.………………………….4分
差数列.………………………….4分
 ,
, ,
, ………………………………8分
………………………………8分

 ,
, …………
………… ………………………2分
………………………2分所以
 是以1为首
是以1为首 项,4为公差的等
项,4为公差的等 差数列.………………………….4分
差数列.………………………….4分 ,
, ,
, ………………………………8分
………………………………8分
略

练习册系列答案
相关题目
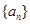 满足
满足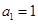 ,
,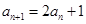 ,则数列
,则数列



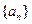 是递增数列,且满足
是递增数列,且满足 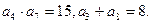
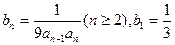 ,求数列
,求数列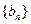 的前
的前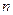 项和
项和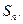
 n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
n∈N*, Sn,Sn+1,Sn+2不构成等比数列. 中,
中, 是数列
是数列 项和,对任意
项和,对任意 ,有
,有
 的值;
的值; 的通项公式是
的通项公式是 ,前
,前 ,求证:对于任意的正整数
,求证:对于任意的正整数 .
. 的前n项和为Sn,且
的前n项和为Sn,且 .
.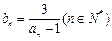 ,求
,求 .
.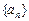 中,满足
中,满足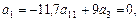 则该数列前
则该数列前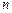 项和
项和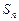 的最小值是 .
的最小值是 . 的前
的前 项和为
项和为 ,若
,若 ,则
,则 等于 ( )
等于 ( )