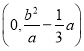题目内容
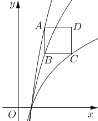
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() ,
,![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)若函数![]() 存在唯一零点
存在唯一零点![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)1;(2)![]() .
.
【解析】
(1)当![]() 时,求得
时,求得![]() ,根据导数求得函数的单调性,进而求得函数的最大值,得到答案.
,根据导数求得函数的单调性,进而求得函数的最大值,得到答案.
(2)求得![]() ,分类讨论求得函数的单调区间,结合题意和函数零点的概念,即可求解.
,分类讨论求得函数的单调区间,结合题意和函数零点的概念,即可求解.
(1)当![]() 时,函数
时,函数![]() ,则
,则![]() ,
,
当![]() 或
或![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
又由![]() ,
,![]() ,
,
所以![]() 时,
时,![]() 的最大值为1.
的最大值为1.
(2)由函数![]() ,则
,则![]() ,
,
①当![]() 时,由
时,由![]() ,得
,得![]() 或
或![]() ,
,![]() 在
在![]() 上是增函数,
上是增函数,
又由![]() ,
,![]() ,
,
∴![]() 在
在![]() 上有零点,不合题意,
上有零点,不合题意,
②当![]() 时,
时,![]() 有两个实数根,即函数
有两个实数根,即函数![]() 有两个零点,不合题意,
有两个零点,不合题意,
③当![]() 时,由
时,由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() 或
或![]() ,
,
所以函数![]() 单调增区间为
单调增区间为![]() ,单调减区间为
,单调减区间为![]() ,
,![]() ,
,
因为函数![]() 存在唯一零点
存在唯一零点![]() ,且
,且![]() ,
,
则满足![]() ,即
,即![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
又由![]()
![]() ,且
,且![]() ,
,
所以![]() 有唯一零点
有唯一零点![]() ,且
,且![]() ,
,
所以实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
【题目】某校高二理科1班共有50名学生参加学业水平模拟考试,成绩(单位:分,满分100分)大于或等于90分的为优秀,其中语文成绩近似服从正态分布![]() ,数学成绩的频率分布直方图如图.
,数学成绩的频率分布直方图如图.
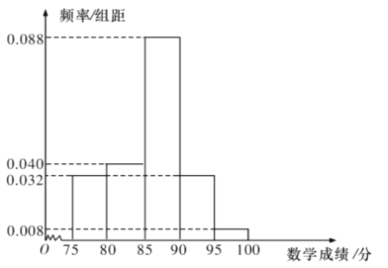
(1)这50名学生中本次考试语文、数学成绩优秀的大约各有多少人?
(2)如果语文和数学两科成绩都优秀的共有4人,从语文优秀或数学优秀的这些同学中随机抽取3人,设3人中两科都优秀的有X人,求X的分布列和数学期望;
(3)根据(1)(2)的数据,是否有99%以上的把握认为语文成绩优秀的同学,数学成绩也优秀?
语文优秀 | 语文不优秀 | 合计 | |
数学优秀 | |||
数学不优秀 | |||
合计 |
附:①若![]() ,则
,则![]() ,
,![]() ;②
;②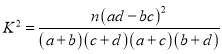 ;
;
③
| 0.1 | 0.05 | 0.025 | 0.010 | p>0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |