题目内容
6.如图一,在四边形PEBC中,PC=1,CB=$\sqrt{3}$,∠CPE=$\frac{π}{3}$,∠PCB=$\frac{5π}{6}$,在边PE上取一点A,使PA=1(PE足够长),连结AC、AB,将△PAC与△EAB分别沿AC和AB折起,使平面PAC⊥平面ABC,且PE∥BC(如图二);过BC作平面交AP、AE分别于点M、N.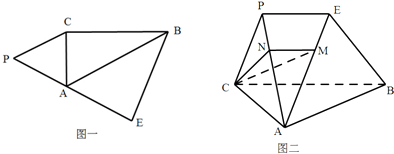
(1)求证:MN∥PE;
(2)设$\frac{AN}{AP}$=λ,求λ 的值,使得平面ABC与平面MNC所成的锐二面角的大小为45°.
分析 (1)利用线面平行的判定定理证明BC∥平面APE,可得MN∥PE;
(2)证明∠NCA为二面角N-CB-A的平面角,可得∠NCA=45°.在△NCA中运用正弦定理得,$\frac{AN}{AC}$=$\frac{sin45°}{sin75°}$=$\sqrt{3}$-1,即可求λ 的值.
解答 (1)证明:因为PE∥CB,BC?平面APE,PE?平面APE,
所以BC∥平面APE …(3分)
又依题意平面ABC交平面APE于MN,故MN∥BC,所以MN∥PE …(5分)
(2)解:由(1)知MN∥BC,故C、B、M、N共面,平面ABC与平面MNC所成的锐二面角即N-CB-A.
因为平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,且CB⊥AC,
所以CB⊥平面PAC.故CB⊥CN,即知∠NCA为二面角N-CB-A的平面角…(11分),
所以∠NCA=45°.
在△NCA中运用正弦定理得,$\frac{AN}{AC}$=$\frac{sin45°}{sin75°}$=$\sqrt{3}$-1.
所以,λ=$\frac{AN}{AP}$=$\sqrt{3}$-1. …(13分)
点评 本题考查线面平行的判定与性质,考查二面角的平面角,考查正弦定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
14.已知直线(3-7a+2a2)x-(9-a2)y+3a2=0的倾斜角的正弦为$\frac{{\sqrt{2}}}{2}$,则a的值为( )
| A. | $-\frac{2}{3}$或4 | B. | 3或$-\frac{2}{3}$ | C. | $-\frac{2}{3}$ | D. | 不存在 |
1.有以下四个命题,正确的是( )
| A. | 在空间,如果一个角的两边与另一个角的两边分别平行,那么这两个角相等 | |
| B. | 分别和两条异面直线都相交的两条直线可能是相交直线 | |
| C. | 若直线a在平面α外,则直线a与平面α内的所有直线都没有公共点 | |
| D. | 若直线a上有两点到平面α的距离为1,则a∥α |
18.把长度为16的线段分成两段,各围成一个正方形,它们的面积和最小值为( )
| A. | 2 | B. | 4 | C. | 5 | D. | 8 |
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2PD,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2PD,PD⊥底面ABCD.