题目内容
15. 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2PD,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2PD,PD⊥底面ABCD.(1)证明:PA⊥BD;
(2)若PD=AD,求PA与面PBD所成的角.
分析 (1)设AB=2AD=2PD=2,由余弦定理得BD=$\sqrt{3}$,由勾股定理得AD⊥BD,由线面垂直得BD⊥PD,由此能证明BD⊥平面PAD,从而得到PA⊥BD.
(2)以D为原点,DA为x轴,DB为y轴,DP为z轴,建立空间直角坐标系,利用向量法能求出PA与面PBD所成的角.
解答 (1)证明:∵四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2PD,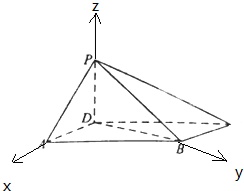
∴设AB=2AD=2PD=2,则BD=$\sqrt{4+1-2×2×1×cos60°}$=$\sqrt{3}$,
∴AD2+BD2=AB2,∴AD⊥BD,
∵PD⊥底面ABCD,BD?平面ABCD,∴BD⊥PD,
∵AD∩PD=D,∴BD⊥平面PAD,
∵BD?平面PAD,∴PA⊥BD.
(2)解:以D为原点,DA为x轴,DB为y轴,DP为z轴,建立空间直角坐标系,
设设AB=2AD=2PD=2,则P(0,0,1),A(1,0,0),$\overrightarrow{PA}$=(1,0,-1),
平面PBD的法向量$\overrightarrow{n}$=(1,0,0),
设PA与面PBD所成的角为θ,
则sinθ=|cos<$\overrightarrow{n},\overrightarrow{PA}$>|=|$\frac{\overrightarrow{n}•\overrightarrow{PA}}{|\overrightarrow{n}|•|\overrightarrow{PA}|}$|=|$\frac{1}{\sqrt{2}}$|=$\frac{\sqrt{2}}{2}$.
∴θ=$\frac{π}{4}$,即PA与面PBD所成的角为$\frac{π}{4}$.
点评 本题考查异面直线垂直的证明,考是查线面角的大小的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | y=sin($\frac{1}{3}$x+$\frac{π}{6}$) | B. | y=sin(3x+$\frac{π}{6}$) | C. | y=sin($\frac{1}{3}$x-$\frac{π}{6}$) | D. | y=sin(3x-$\frac{π}{6}$) |
| A. | (-$∞,\frac{3}{4}$)∪($\frac{5}{4},+∞$) | B. | (-$∞,\frac{3}{4}$]∪[$\frac{5}{4},+∞$) | C. | [$\frac{3}{4},\frac{5}{4}$] | D. | ($\frac{3}{4},\frac{5}{4}$) |
| A. | (0,2) | B. | (-$\frac{3}{2}$,0) | C. | (-2,3) | D. | (-2,2) |