题目内容
【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是![]() 的中点.
的中点.
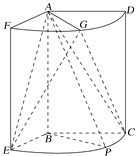
(1)设P是![]() 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;
(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析: (1)第(1)问,直接证明BE⊥平面ABP得到BE⊥BP,从而求出∠CBP的大小. (2)第(2)问,可以利用几何法求,也可以利用向量法求解.
试题解析:
(1)

因为AP⊥BE,AB⊥BE,AB,AP平面ABP,AB∩AP=A,所以BE⊥平面ABP.
又BP平面ABP,所以BE⊥BP.又∠EBC=120°,所以∠CBP=30°.
(2)方法一:如图,取![]() 的中点H,连接EH,GH,CH.
的中点H,连接EH,GH,CH.
因为∠EBC=120°,所以四边形BEHC为菱形,
所以AE=GE=AC=GC=![]() .
.
取AG的中点M,连接EM,CM,EC,
则EM⊥AG,CM⊥AG,
所以∠EMC为所求二面角的平面角.
又AM=1,所以EM=CM=![]() .
.
在△BEC中,由于∠EBC=120°,
由余弦定理得EC2=22+22-2×2×2×cos 120°=12,
所以EC=2![]() ,所以△EMC为等边三角形,
,所以△EMC为等边三角形,
故所求的角为60°.
方法二:

以B为坐标原点,分别以BE,BP,BA所在的直线为x,y,z轴,建立如图所示的空间直角坐标系B-xyz.
由题意得A(0,0,3),E(2,0,0),G(1, ![]() ,3),C(-1,
,3),C(-1, ![]() ,0),
,0),
故![]() =(2,0,-3),
=(2,0,-3), ![]() =(1,
=(1, ![]() ,0),
,0), ![]() =(2,0,3).
=(2,0,3).
设![]() =(x1,y1,z1)是平面AEG的一个法向量,
=(x1,y1,z1)是平面AEG的一个法向量,
由![]() 可得
可得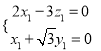
取z1=2,可得平面AEG的一个法向量![]() =(3,-
=(3,- ![]() ,2).
,2).
设![]() =(x2,y2,z2)是平面ACG的一个法向量.
=(x2,y2,z2)是平面ACG的一个法向量.
由![]() 可得
可得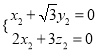
取z2=-2,得平面ACG的一个法向量n=(3,- ![]() ,-2).
,-2).
所以cos〈![]() 〉=
〉=![]() =
=![]() .
.
故所求的角为60°.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案【题目】某市2011年至2017年新开楼盘的平均销售价格(单位:千元/平方米)的统计数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格 | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求![]() 关于x的线性回归方程;
关于x的线性回归方程;
(2)利用(1)中的回归方程,分析2011年至2017年该市新开楼盘平均销售价格的变化情况,并预测该市2019年新开楼盘的平均销售价格。
附:参考公式:  ,
,![]() ,其中
,其中![]() 为样本平均值。
为样本平均值。
参考数据:![]()
![]() .
.

