题目内容
已知曲线 :
: 和
和 :
: 的焦点分别为
的焦点分别为 、
、 ,点
,点 是
是 和
和 的一个交点,则△
的一个交点,则△ 的形状是( )
的形状是( )
 :
: 和
和 :
: 的焦点分别为
的焦点分别为 、
、 ,点
,点 是
是 和
和 的一个交点,则△
的一个交点,则△ 的形状是( )
的形状是( )| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.都有可能 |
B
试题分析:
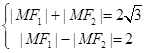 ,即
,即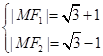 ,而
,而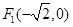 ,
,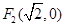 ,
,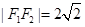 ,
,∴
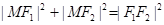 ,∴
,∴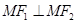 ,∴△
,∴△ 的形状是直角三角形.
的形状是直角三角形.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
 :
: 和
和 :
: 的焦点分别为
的焦点分别为 、
、 ,点
,点 是
是 和
和 的一个交点,则△
的一个交点,则△ 的形状是( )
的形状是( )| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.都有可能 |
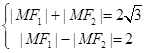 ,即
,即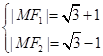 ,而
,而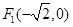 ,
,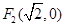 ,
,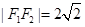 ,
,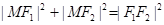 ,∴
,∴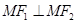 ,∴△
,∴△ 的形状是直角三角形.
的形状是直角三角形.
 名校课堂系列答案
名校课堂系列答案