Question

集合A={x|-1＜x＜3}，B={y|-1≤y≤2}，计算在不同条件下，x、y分别在所指定范围内随机取值，求y≥x（记作事件A）的概率P（A）．
（Ⅰ）当x∈A∩Z，y∈B∩Z时；
（Ⅱ）当x∈A，y∈B时．

Answer 1

分析：（1）列举出所有的可能的数对，共有12个，看清要求满足的条件：“y≥x”，写出所有的数对，要做到不重不漏．
（2）本小题是一个几何概型的概率问题，先根据全部结果的区域为{（x，y）|-1＜x＜3，-1≤y≤2}，是一个矩形区域，做出面积，再计算满足y≥x是一个三角形区域面积，利用几何概型计算公式得到结果．

解答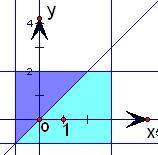：解：（Ⅰ）A∩Z={0，1，2}，B∩Z={-1，0，1，2}
基本事件的总数为：（0，-1），（0，0），（0，1），（0，2），（1，-1），（1，0），（1，1），（1，2），（2，-1），（2，0），（2，1），（2，2）共12 个．
y≥x有6个（0，0），（0，1），（0，2），（1，1），（1，2），（2，2），
∴P（A）=

6

12

=0.5…（6分）
（Ⅱ） 全部结果的区域为{（x，y）|-1＜x＜3，-1≤y≤2}，是一个矩形区域，面积为12，
满足y≥x是一个三角形区域，面积为

9

2

．
∴P(A)=

9/2

4×3

=

3

8

…（12分）

点评：古典概型和几何概型是我们学习的两大概型，古典概型要求能够列举出所有事件和发生事件的个数，而不能列举的就是几何概型，几何概型的概率的值是通过长度、面积、和体积的比值得到．