Question

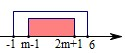
设集合A={x|-1≤x≤6}，B={x|m-1≤x≤2m+1}，已知B⊆A，求实数m的取值范围．

Answer 1

分析：讨论集合B为空集和非空时，利用B⊆A，确定m的取值范围即可．

解答：解：若B=∅，则m-1＞2m+1，即m＜-2时，满足B⊆A．
若B≠∅，则m-1≤2m+1，即m≥-2时，
若B⊆A，则

m-1≥-1 2m+1≤6

，
即

m≥0 m≤ 5 2

，
∴0≤m≤

5

2

，
综上：m＜-2或0≤m≤

5

2

．

点评：本题主要考查集合关系的应用，注意要对集合B进行分类讨论．