题目内容
设p:
≤
,q:关于x的不等式x2-4x+m2≤0的解集是空集,试确定实数m的取值范围,使得p∨q为真命题,p∧q为假命题.
| m-2 |
| m-3 |
| 2 |
| 3 |
| m-2 |
| m-3 |
| 2 |
| 3 |
由不等式x2-4x+m2≤0的解集是空集,得△=16-4m2<0⇒m<-2或m>2.
由复合命题真值表知,若p∨q真,p∧q假,则命题p、q一真一假,
当p真q假时,即
|
当p假q真时,即
|
综上得,m∈(-∞,-2)∪[0,2]∪[3,+∞).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
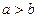 ,则
,则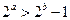 ”的否命题为 。
”的否命题为 。