题目内容
已知p:?x∈R,mx2+1≤0,q:?x∈R,x2+mx+1>0,若p∨q为假命题,则实数m的取值范围为( )
| A.m≥2 | B.m≤-2 | C.m≤-2或m≥2 | D.-2≤m≤2 |
由p:?x∈R,mx2+1≤0,可得m<0,
由q:?x∈R,x2+mx+1>0,可得△=m2-4<0,解得-2<m<2
因为pVq为假命题,所以p与q都是假命题
若p是假命题,则有m≥0;若q是假命题,则有m≤-2或m≥2
故符合条件的实数m的取值范围为m≥2
故选A
由q:?x∈R,x2+mx+1>0,可得△=m2-4<0,解得-2<m<2
因为pVq为假命题,所以p与q都是假命题
若p是假命题,则有m≥0;若q是假命题,则有m≤-2或m≥2
故符合条件的实数m的取值范围为m≥2
故选A

练习册系列答案
相关题目
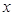 为非零实数,则
为非零实数,则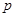 :
: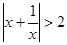 是
是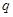 :
: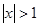 成立的 ( )
成立的 ( )