题目内容
我市为积极相应《全民健身条例》大力开展学生体育活动,如图是委托调查机构在市区的两所学校A校、B校中分别随机抽取了10名高二年级的学生当月体育锻炼时间的茎叶图(单位:小时)
(Ⅰ)根据茎叶图,分别写将两所学校学生当月体育锻炼 时间的众数、中位数和平均数填入下表;
(Ⅱ)根据茎叶图,求A校学生的月体育锻炼时间的方差;
(Ⅲ)若学生月体育锻炼的时间低于10小时,就说明该生体育锻炼时间严重不足。根据茎叶图估计 两所学校的学生体育锻炼严重不足的频率。
两所学校的学生体育锻炼严重不足的频率。
(Ⅰ)见解析;(Ⅱ)30.2;(Ⅲ)A校的频率为0.2,B校的频率,0.5.
解析试题分析:(Ⅰ)...................6分 A校 B校 众数 17 13或14 中位数 14 8 平均数 13 11
(Ⅱ) ...................7分
...................7分 ...........................10分
...........................10分
(Ⅲ)A校的频率为 .......................11分
.......................11分
B校的频率为 .................................12分
.................................12分
考点:众数、中位数、平均数、方差的概念;茎叶图。
点评:本题直接考查众数、中位数、平均数、方差等有关概念,属于基础题型。但我们要熟记方差公式。

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
(10分)某种产品的广告费支出x与消费额y(单位:百万元)之间有如下对应数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)预测当广告费支出为700万元时的销售额.
(本题14分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量( 吨)与相应的生产能耗
吨)与相应的生产能耗 (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
 | 3 | 4 | 5 | 6 |
 | 2.5 | 3 | 4 | 4.5 |
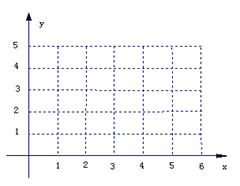
(1)请画出上表数据的散点图;并指出x,y 是否线性相关;
(2)请根据上表提供的数据,用最小二乘法求出
 关于
关于 的线性回归方程
的线性回归方程 ;
;(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式
 ,
, )
) 某校为了解学生的学科学习兴趣,对初高中学生做了一个喜欢数学和喜欢语文的抽样调查,随机抽取了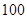 名学生,相关的数据如下表所示:
名学生,相关的数据如下表所示:
| | 数学 | 语文 | 总计 |
| 初中 | 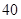 | 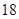 | 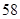 |
| 高中 | 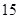 | 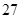 | 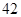 |
| 总计 | 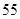 | 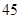 | 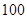 |
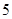 名,高中学生应该抽取几名?
名,高中学生应该抽取几名?(2) 在(1)中抽取的
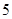 名学生中任取
名学生中任取 名,求恰有
名,求恰有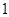 名初中学生的概率.
名初中学生的概率. (本小题满分12分)某种产品的广告费支出 与销售额
与销售额 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
 | 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |
(2)请根据上表提供的数据,用最小二乘法求出
 关于
关于 的线性回归方程
的线性回归方程 .(其中
.(其中 )
) 
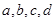 的值;
的值;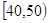 ,
,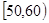 …
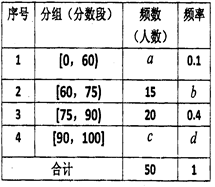
…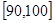 后画出如下频率分布直方图,根据图形中所给的信息,回答以下问题:
后画出如下频率分布直方图,根据图形中所给的信息,回答以下问题: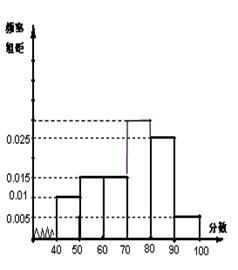
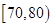 的频率.
的频率.
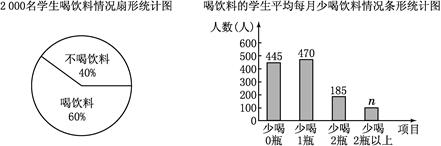
 希望工程?
希望工程?