题目内容
【题目】在平面直角坐标系xOy中,直线l的参数方程为 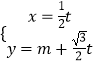 (t为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2﹣2ρcosθ﹣4=0
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2﹣2ρcosθ﹣4=0
(1)若直线l与曲线C没有公共点,求m的取值范围;
(2)若m=0,求直线l被曲线C截得的弦长.
【答案】
(1)解:曲线C的极坐标方程对应的直角坐标方程为x2+y2﹣2x﹣4=0,即(x﹣1)2+y2=5
直线l的参数方程为  ,代入并整理可得t2+(
,代入并整理可得t2+( ![]() m﹣1)t+m2﹣4=0
m﹣1)t+m2﹣4=0
∵直线l与曲线C没有公共点,
∴△=( ![]() m﹣1)2﹣4(m2﹣4)<0,
m﹣1)2﹣4(m2﹣4)<0,
∴m<﹣ ![]() ﹣2
﹣2 ![]() 或m>﹣
或m>﹣ ![]() +2
+2 ![]()
(2)解:若m=0,直线l的极坐标方程为θ= ![]() ,代入C的极坐标方程并整理可得ρ2﹣ρ﹣4=0.
,代入C的极坐标方程并整理可得ρ2﹣ρ﹣4=0.
直线l被曲线C截得的弦的端点的极径分别为ρ1,ρ2,则ρ1+ρ2=1,ρ1ρ2=﹣4,
∴直线l被曲线C截得的弦长=|ρ1﹣ρ2|= ![]() =
= ![]()
【解析】(1)曲线C的极坐标方程化为直角坐标方程,直线l的参数方程为  ,代入并整理可得t2+(
,代入并整理可得t2+( ![]() m﹣1)t+m2﹣4=0,利用直线l与曲线C没有公共点,即可求m的取值范围;(2)若m=0,若m=0,直线l的极坐标方程为θ=
m﹣1)t+m2﹣4=0,利用直线l与曲线C没有公共点,即可求m的取值范围;(2)若m=0,若m=0,直线l的极坐标方程为θ= ![]() ,代入C的极坐标方程并整理可得ρ2﹣ρ﹣4=0,利用极径的意义求直线l被曲线C截得的弦长.
,代入C的极坐标方程并整理可得ρ2﹣ρ﹣4=0,利用极径的意义求直线l被曲线C截得的弦长.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
