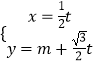题目内容
【题目】已知椭圆![]() 的焦点与双曲线
的焦点与双曲线![]() 的焦点重合,并且经过点
的焦点重合,并且经过点![]() .
.
(Ⅰ)求椭圆C的标准方程;
(II) 设椭圆C短轴的上顶点为P,直线![]() 不经过P点且与
不经过P点且与![]() 相交于
相交于![]() 、
、![]() 两点,若直线PA与直线PB的斜率的和为
两点,若直线PA与直线PB的斜率的和为![]() ,判断直线
,判断直线![]() 是否过定点,若是,求出这个定点,否则说明理由.
是否过定点,若是,求出这个定点,否则说明理由.
【答案】(Ⅰ)![]() ;(II)
;(II)![]() 过定点
过定点![]() 。
。
【解析】
(Ⅰ)推导出![]() ,从而焦点F1(
,从而焦点F1(![]() ,0),F2(
,0),F2(![]() ,0),由椭圆定义得a=2,b=1,由此能求出椭圆的标准方程.
,0),由椭圆定义得a=2,b=1,由此能求出椭圆的标准方程.
(II)先考虑斜率不存在时,不存在两个交点,舍去,斜率存在时设直线l方程为:y=kx+m,A(x1,y1),B(x2,y2),由![]() 得
得![]() 及
及![]() ,代入
,代入![]() 1中,得到m=﹣2k﹣1,代入直线方程即可得到定点.
1中,得到m=﹣2k﹣1,代入直线方程即可得到定点.
(Ⅰ)双曲线的焦点为![]() ,
,![]() ,亦即椭圆C的焦点,
,亦即椭圆C的焦点,
∴![]() ,
,
又椭圆经过点![]() .
.
由椭圆定义得![]() ,
,
解得![]() ,
,![]()
∴椭圆![]() 的方程为:
的方程为:![]() .
.
(II)![]() 当斜率不存在时,设
当斜率不存在时,设![]() ,
,
![]() ,
,
得t=2,此时![]() 过椭圆右顶点,不存在两个交点,故不满足题意.
过椭圆右顶点,不存在两个交点,故不满足题意.
![]() 当斜率存在时,设
当斜率存在时,设![]() ,
,
![]() ,
,
联立![]() ,整理得
,整理得![]() ,
,
![]()
![]() ,
,
![]()
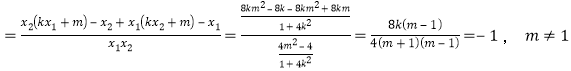 ,
,
![]() ,此时
,此时![]() ,存在
,存在![]() 使得
使得![]() 成立.
成立.
∴直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
当![]() ,
,![]() 时,上式恒成立,所以
时,上式恒成立,所以![]() 过定点
过定点![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目