已知等边三角形ABC与等边三角形BCD所在的平面垂直.且BC=2.则三棱锥A-BCD的体积为( )A．1B．$\sqrt{3}$C．2D．2$\sqrt{3}$ 题目和参考答案——青夏教育精英家教网——

题目内容

12．已知等边三角形ABC与等边三角形BCD所在的平面垂直，且BC=2，则三棱锥A-BCD的体积为（　　）

A．

1

B．

$\sqrt{3}$

C．

2

D．

2$\sqrt{3}$

分析画出图形，求出棱锥的高，底面面积，然后求出体积．

解答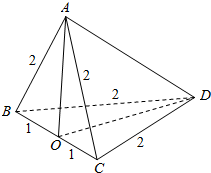解：如图：取BC的中点O，连结AO与OD，底面三角形的面积为：$\frac{1}{2}×2×\sqrt{3}$=$\sqrt{3}$．
三棱锥的体积为：$\frac{1}{3}×\sqrt{3}×\sqrt{3}$=1．
故选：A．

点评本题考查棱锥的体积的求法，考查空间想象能力以及计算能力．

练习册系列答案

天利38套中考试题精粹系列答案

教材解读与拓展系列答案

教材快线系列答案

教材完全学案系列答案

精析巧练系列答案

今日课堂课时作业系列答案

金版卷王课程探究大试卷系列答案

金榜之路系列答案

金点中考系列答案

金海全A突破系列答案

相关题目

2．（1）函数y=sin（2x-$\frac{π}{6}$）图象的条对称轴是方程x=$\frac{kπ}{2}$+$\frac{π}{3}$，k∈Z，对称中心坐标（$\frac{kπ}{2}$+$\frac{π}{12}$，0），k∈Z，最大值x时集合：{x|x=kπ+$\frac{π}{3}$，k∈Z}．
（2）函数y=sin（2x-$\frac{π}{6}$）-1图象的条对称轴是方程x=$\frac{kπ}{2}$+$\frac{π}{3}$，k∈Z，对称中心坐标（$\frac{kπ}{2}$+$\frac{π}{12}$，0），k∈Z，最大值x时集合：{x|x=kπ+$\frac{π}{3}$，k∈Z}．
（3）函数y=tan（2x-$\frac{π}{6}$）+3图象对称中心坐标（ $\frac{kπ}{4}$+$\frac{π}{12}$，0），k∈Z，单调递增区间为[kπ-$\frac{π}{6}$，$\frac{kπ}{2}$+$\frac{π}{3}$]，k∈Z．
（4）函数y=|tan（2x-$\frac{π}{6}$）|+3图象的条对称轴是方程x=$\frac{kπ}{2}$+$\frac{π}{3}$，k∈Z，周期是π，单调递减区间为[kπ-$\frac{π}{6}$，$\frac{kπ}{2}$+$\frac{π}{12}$]，k∈Z．

3．指出当角x取何值时下列函数取得最大值和最小值．
（1）y=sin（3x-$\frac{π}{4}$）；
（2）y=sin2x-cos2x．

20．已知点F为椭圆$\frac{{x}^{2}}{2}$+y²=1的左焦点，过点F的直线l₁ 与椭圆交于P、Q两点，过F且与l₁垂直，直线l₂交椭圆于M，N两点，求四边形PMQN面积的最小值和最大值．

7．函数y=3sin（$\frac{x}{2}$-$\frac{π}{8}$）的振幅、周期、初相分别为（　　）

-3，4π，$\frac{π}{8}$

3，4π，-$\frac{π}{8}$

3，π，-$\frac{π}{8}$

-3，π，$\frac{π}{8}$

17．已知sinα+cosα=-$\frac{1}{3}$，其中0＜α＜π，求sinα-cosα的值．

4．在直角坐标系中，有一条长度为2的线段AB，点A在y轴上运动，点B在x轴上运动，且保持线段长度不变，线段AB上的点P分线段AB所成的比为1：2，求点P满足的方程．

1．2014年小明以优异的成绩研究生毕业，并获得一份待遇优厚的工作．从2015年起，每年元月在银行存入5万元，打算连续存十年，银行年利率为r（按复利计算），到2025年元月取出的本利之和是$\frac{5（1{+r）}^{11}-5-5r}{r}$．

2．若函数f（x）=3+log₂x的图象与函数g（x）的图象关于y=x对称，则函数g（x）=2^x-3．