题目内容
函数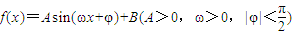 的图象上一个最高点的坐标为
的图象上一个最高点的坐标为 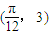 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为 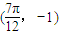 .
.(Ⅰ)求f(x)的表达式;
(Ⅱ) 当
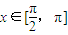 ,求函数f(x)的单调递增区间和零点.
,求函数f(x)的单调递增区间和零点.
【答案】分析:(I)由已知中函数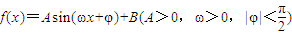 的图象上一个最高点的坐标为
的图象上一个最高点的坐标为 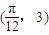 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为 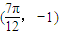 .我们可根据两个最值点的纵坐标求出A,B的值,根据横坐标求出周期T,进而得到ω及φ的值,从而求出求f(x)的表达式;
.我们可根据两个最值点的纵坐标求出A,B的值,根据横坐标求出周期T,进而得到ω及φ的值,从而求出求f(x)的表达式;
(Ⅱ)根据由(1)的结论,及正弦型函数单调区间的求法,及零点的定义,我们易得到结论.
解答:解:(Ⅰ)依题意的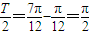 ,所以T=π,于是
,所以T=π,于是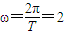 (2分)
(2分)
由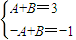 解得
解得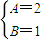 (4分)
(4分)
把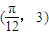 代入f(x)=2sin(2x+φ)+1,可得
代入f(x)=2sin(2x+φ)+1,可得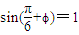 ,所以
,所以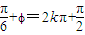 ,
,
所以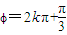 ,因为
,因为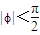 ,所以
,所以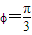
综上所述,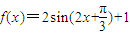 (7分)
(7分)
(Ⅱ)令f(x)=0,得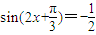 ,又∵
,又∵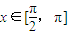
∴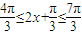 ∴
∴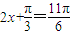 故
故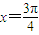 函数f(x)的零点是
函数f(x)的零点是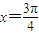 (10分)
(10分)
∵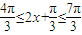 ∴由
∴由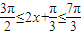 得
得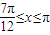 ∴函数f(x)的单调递增区间是
∴函数f(x)的单调递增区间是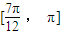 (13分)
(13分)
点评:本题考查的知识点是由y=Asin(ωx+φ)的部分图象确定其解析式,正弦型函数的性质及函数的零点,其中根据已知中的条件求出函数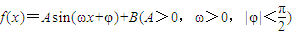 的解析式,是解答本题的关键.
的解析式,是解答本题的关键.
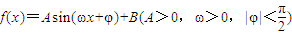 的图象上一个最高点的坐标为
的图象上一个最高点的坐标为 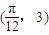 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为 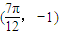 .我们可根据两个最值点的纵坐标求出A,B的值,根据横坐标求出周期T,进而得到ω及φ的值,从而求出求f(x)的表达式;
.我们可根据两个最值点的纵坐标求出A,B的值,根据横坐标求出周期T,进而得到ω及φ的值,从而求出求f(x)的表达式;(Ⅱ)根据由(1)的结论,及正弦型函数单调区间的求法,及零点的定义,我们易得到结论.
解答:解:(Ⅰ)依题意的
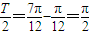 ,所以T=π,于是
,所以T=π,于是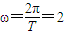 (2分)
(2分)由
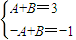 解得
解得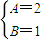 (4分)
(4分)把
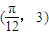 代入f(x)=2sin(2x+φ)+1,可得
代入f(x)=2sin(2x+φ)+1,可得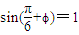 ,所以
,所以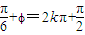 ,
,所以
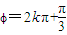 ,因为
,因为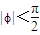 ,所以
,所以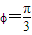
综上所述,
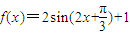 (7分)
(7分)(Ⅱ)令f(x)=0,得
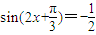 ,又∵
,又∵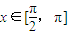
∴
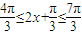 ∴
∴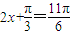 故
故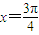 函数f(x)的零点是
函数f(x)的零点是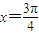 (10分)
(10分)∵
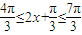 ∴由
∴由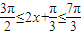 得
得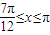 ∴函数f(x)的单调递增区间是
∴函数f(x)的单调递增区间是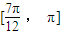 (13分)
(13分)点评:本题考查的知识点是由y=Asin(ωx+φ)的部分图象确定其解析式,正弦型函数的性质及函数的零点,其中根据已知中的条件求出函数
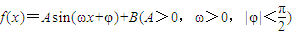 的解析式,是解答本题的关键.
的解析式,是解答本题的关键. 
练习册系列答案
相关题目
 =(1,cos⊙x),
=(1,cos⊙x), =(sin⊙x,
=(sin⊙x,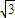 )(⊙>o),函数f(x)=
)(⊙>o),函数f(x)= 的图象上一个最高点的坐标为(
的图象上一个最高点的坐标为( ,2),与之相邻的一个最低点的坐标(
,2),与之相邻的一个最低点的坐标( ,-2).
,-2).