题目内容

函数f(x)=Asin(ωx+φ)+B(A＞0，ω＞0，|φ|＜
π
2
)的图象上一个最高点的坐标为 (
π
12
，3)，与之相邻的一个最低点的坐标为 (
7π
12
，-1)．
（Ⅰ）求f（x）的表达式；
（Ⅱ） 当x∈[
π
2
，π]，求函数f（x）的单调递增区间和零点．
分析：（I）由已知中函数f(x)=Asin(ωx+φ)+B(A＞0，ω＞0，|φ|＜
π
2
)的图象上一个最高点的坐标为 (
π
12
，3)，与之相邻的一个最低点的坐标为 (
7π
12
，-1)．我们可根据两个最值点的纵坐标求出A，B的值，根据横坐标求出周期T，进而得到ω及φ的值，从而求出求f（x）的表达式；
（Ⅱ）根据由（1）的结论，及正弦型函数单调区间的求法，及零点的定义，我们易得到结论．
解答：解：（Ⅰ）依题意的
T
2
=
7π
12
-
π
12
=
π
2
，所以T=π，于是ω=
2π
T
=2（2分）
由
A+B=3
-A+B=-1
解得
A=2
B=1
（4分）
把(
π
12
，3)代入f（x）=2sin（2x+φ）+1，可得sin(
π
6
+?)=1，所以
π
6
+?=2kπ+
π
2
，
所以?=2kπ+
π
3
，因为|?|＜
π
2
，所以?=
π
3

综上所述，f(x)=2sin(2x+
π
3
)+1（7分）
（Ⅱ）令f（x）=0，得sin(2x+
π
3
)=-
1
2
，又∵x∈[
π
2
，π]
∴
4π
3
≤2x+
π
3
≤
7π
3
∴2x+
π
3
=
11π
6
故x=
3π
4
函数f（x）的零点是x=
3π
4
（10分）
∵
4π
3
≤2x+
π
3
≤
7π
3
∴由
3π
2
≤2x+
π
3
≤
7π
3
得
7π
12
≤x≤π∴函数f（x）的单调递增区间是[
7π
12
 ， π]（13分）
点评：本题考查的知识点是由y=Asin（ωx+φ）的部分图象确定其解析式，正弦型函数的性质及函数的零点，其中根据已知中的条件求出函数f(x)=Asin(ωx+φ)+B(A＞0，ω＞0，|φ|＜
π
2
)的解析式，是解答本题的关键．
练习册系列答案
相关题目
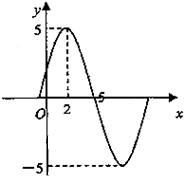精英家教网已知函数f(x)=Asin(ωx+φ)(A＞0，ω＞0，|φ|＜
π2
)的部分图象如图所示．
（1）求函数f（x）的解析式；
（2）若图象g（x）与函数f（x）的图象关于点P（4，0）对称，求函数g（x）的单调递增区间．
（2013•大连一模）已知函数f(x)=Asin(ωx+φ)(x∈R，A＞0，ω＞0，|φ|＜
π
2
)的图象（部分）如图所示，则ω，φ分别为（　　）
当x∈[-
π
6
，
2π
3
]时，函数f(x)=Asin(ωx+θ) (A＞0，ω＞0，|θ|＜
π
2
)的图象如图所示．
（1）求函数f（x）在[-
π
6
，
2π
3
]上的表达式；
（2）求方程f(x)=
2
2
在[-
π
6
，
2π
3
]的解集．
精英家教网函数f(x)=Asin(ωx+φ)，x∈R(A＞0，ω＞0，|φ|＜
π
2
)的一段图象如图5所示：将y=f（x）的图象向右平移m（m＞0）个单位，可得到函数y=g（x）的图象，且图象关于原点对称，g(
π
2013
)＞0．
（1）求A、ω、φ的值；
（2）求m的最小值，并写出g（x）的表达式；
（3）若关于x的函数y=g(
tx
2
)在区间[-
π
3
，
π
4
]上最小值为-2，求实数t的取值范围．
精英家教网已知函数f(x)=Asin(ωx+φ)(A＞0，ω＞0，x∈R，|φ|＜
π
2
)的图象（部分）如图所示，则f（x）的解析式是（　　）
A、f(x)=5sin(
π
3
x+
π
6
)
B、f(x)=5sin(
π
6
x-
π
6
)
C、f(x)=5sin(
π
6
x+
π
6
)
D、f(x)=5sin(
π
3
x-
π
6
)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网