题目内容
（本小题满分12分）
已知数列
的前
项和为
，满足
.
（1）求证：数列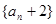
为等比数列；
（2）若数列
满足
，
为数列
的前项和，求证：
.
（1）
.
（2）先“错位相减法”求和，放缩即得
.
解析试题分析：（1）由
得
，
，
，
，
为等比数列，首项
，公比为2.
.
（2）
，
， 
，
，
，
.
考点：本题主要考查等差数列、等比数列的的基础知识，“错位相减法”，不等式证明的放缩法。
点评：中档题，本题具有较强的综合性，本解答从确定通项公式入手，进一步认识数列的特征，利用“错位相减法”达到求和目的，最后通过放缩实现不等式证明。“分组求和法”“裂项相消法”也是常常考到的求和方法。
练习册系列答案
相关题目
是等差数列，
是否是等差数列，并说明理由；
，试写出数列
，问是否存在这样的实数
，使
时取得最大值。若存在，求出
,数列
满足
,数列
满足
；又知数列
中，
，且对任意正整数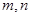
，
.
项，第
项，第
项，……，第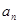
项，……删去后，剩余的项按从小到大的顺序排成新数列
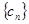，求数列
项和.
的前
项和
，数列
满足
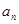;（2）求数列
;
恒成立
满足
.
是等差数列；
，求数列
的前
项和
.
的前n项和
（n为正整数）。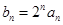
，求证数列
是等差数列，并求数列
，
试比较
与
的大小，并予以证明。
+
+…+
] （n≥2，n∈N）
=
）（1+
）…（1+
）<4
是各项均不为
的等差数列，公差为
，
为其前
项和，且满足
，
．数列
满足
，
为数列
和数列
的前n项和
；
，不等式
恒成立，求实数
的取值范围；
的前
项和为
，且
；数列
为等差数列，且
，
.
，
为数列
的前