题目内容
已知平面向量a、b、c的模均为1,它们相互之间的夹角均为120°,记f(x)=|xa+b+c|.(1)求f(x)的表达式;
(2)试画出函数y=(
)f(x)的图象.
解:(1)［f(x)］2=(xa+b+c)2
=x2a2+b2+c2+2xa·b+2xa·c+2b·c,
∵|a|=|b|=|c|=1,a·b=a·c=b·c=cos120°=-
,
∴［f(x)］2=x2+2-2x-1
=x2-2x+1=(x-1)2.
∴f(x)=|x-1|.
(2)y=(
)f(x)=(
)|x-1|
=
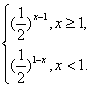
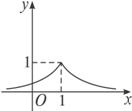
图象如图所示.
练习册系列答案
相关题目