题目内容
已知平面向量
,
满足
•(
+
)=3,且|
|=2,|
|=1,则向量
与
的夹角为
.
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| 2π |
| 3 |
| 2π |
| 3 |
分析:设向量
与
的夹角为θ,θ∈[0,π],由
•(
+
)=3可得
2+
•
=3,代入数据可得关于cosθ的方程,解之结合θ的范围可得.
| a |
| b |
| a |
| a |
| b |
| a |
| a |
| b |
解答:解:设向量
与
的夹角为θ,θ∈[0,π]
由
•(
+
)=3可得
2+
•
=3,
代入数据可得22+2×1×cosθ=3,
解之可得cosθ=-
,
故可得θ=
故答案为:
| a |
| b |
由
| a |
| a |
| b |
| a |
| a |
| b |
代入数据可得22+2×1×cosθ=3,
解之可得cosθ=-
| 1 |
| 2 |
故可得θ=
| 2π |
| 3 |
故答案为:
| 2π |
| 3 |
点评:本题考查数量积与两个向量的夹角的关系,属基础题.

练习册系列答案
相关题目
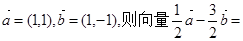 ( )
( )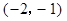 B.
B.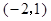 C.
C.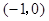 D.
D.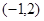
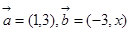 ,且
,且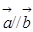 ,则
,则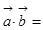 (
)
(
)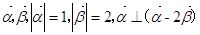 则
则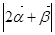 的值是( )
的值是( ) 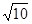 C.
C. 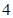 D.
D.
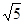
 ,则
,则 ( )
( )