题目内容
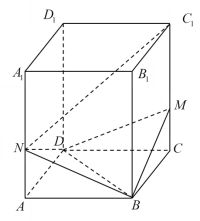
【题目】在平行六面体ABCD﹣A1B1C1D1中,所有棱长均为2,∠AA1D1=∠AA1B1=60°,∠D1A1B1=90°.
(1)求证:A1C⊥B1D1;
(2)求对角线AC1的长;
(3)求二面角C1﹣AB1﹣D1的平面角的余弦值的大小.
【答案】(1)证明见详解;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据题意,先证明B1D1⊥平面A1ACC1,再根据线面垂直推证线线垂直即可;
(2)由![]() 平面
平面![]() 推证出
推证出![]() 为直角三角形,再用勾股定理求解即可;
为直角三角形,再用勾股定理求解即可;
(3)以![]() 为坐标原点,建立空间直角坐标系,分别求出两个平面的法向量,再根据向量夹角的求解公式,即可求得.
为坐标原点,建立空间直角坐标系,分别求出两个平面的法向量,再根据向量夹角的求解公式,即可求得.
(1)证明:∵在平行六面体ABCD﹣A1B1C1D1中,所有棱长均为2,
∴AD1=AB1=2,连结A1C1,B1D1,交于点O,连结AO,如下图所示:
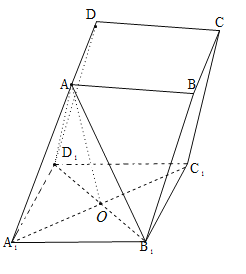
∵∠AA1D1=∠AA1B1=60°,∠D1A1B1=90°.∴AO⊥B1D1,
∵四边形A1B1C1D1为正方形,∴B1D1⊥A1C1,
∴B1D1⊥平面A1ACC1,
∵A1C平面A1ACC1,
∴B1D1⊥A1C.
(2)在△AB1D1中,AO![]()
又![]() ,AA1=2,
,AA1=2,
∴![]() ,∴AO⊥A1O,
,∴AO⊥A1O,
∵AO⊥B1D1,∴AO⊥平面A1B1C1D1,
∴AO⊥OC1,
∴AC1![]() 2.
2.
(3)由(2)知AO⊥平面A1B1C1D1,
以点O为原点,OA1为x轴,OB1为y轴,OA为z轴,建立空间直角坐标系,
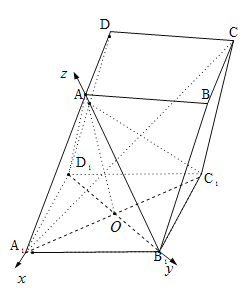
A(0,0,![]() ),B1(0,
),B1(0,![]() ,0),C1(
,0),C1(![]() ,0,0),
,0,0),
![]() (0,
(0,![]() ),
),![]() (
(![]() ,0,
,0,![]() ),
),
设平面AB1C1的法向量![]()
则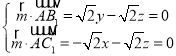 ,
,
取x=1,得![]() (1,﹣1,﹣1),
(1,﹣1,﹣1),
平面AB1D1的法向量![]() (1,0,0),
(1,0,0),
设二面角C1﹣AB1﹣D1的平面角为θ,
则cosθ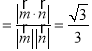 .
.
∴二面角C1﹣AB1﹣D1的平面角的余弦值为![]() .
.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目