题目内容
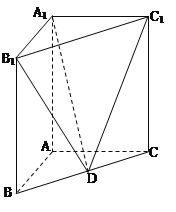
【题目】中国古代数学经典《数书九章》中,将底面为矩形且有一条侧棱与底面垂直的四棱锥称为“阳马”,将四个面都为直角三角形的四面体称之为“鳖臑”.在如图所示的阳马![]() 中,底面ABCD是矩形.
中,底面ABCD是矩形.![]() 平面
平面![]() ,
,![]() ,
,![]() ,以
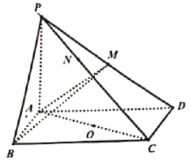
,以![]() 的中点O为球心,AC为直径的球面交PD于M(异于点D),交PC于N(异于点C).
的中点O为球心,AC为直径的球面交PD于M(异于点D),交PC于N(异于点C).
(1)证明:![]() 平面
平面![]() ,并判断四面体MCDA是否是鳖臑,若是,写出它每个面的直角(只需写出结论);若不是,请说明理由;
,并判断四面体MCDA是否是鳖臑,若是,写出它每个面的直角(只需写出结论);若不是,请说明理由;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析,是,![]() ,
,![]() ,
,![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)根据![]() 是球的直径,则
是球的直径,则![]() ,又
,又![]() 平面
平面![]() , 得到
, 得到![]() ,再由线面垂直的判定定理得到
,再由线面垂直的判定定理得到![]() 平面
平面![]() ,,进而得到
,,进而得到![]() ,再利用线面垂直的判定定理得到
,再利用线面垂直的判定定理得到![]() 平面
平面![]() .
.
(2)以A为原点,![]() ,
,![]() ,
,![]() 所在直线为x,y,z轴建立直角坐标系,设
所在直线为x,y,z轴建立直角坐标系,设![]() ,由
,由![]() ,解得
,解得![]() ,得到
,得到![]() ,从而得到
,从而得到![]() ,然后求得平面
,然后求得平面![]() 的一个法向量,代入公式
的一个法向量,代入公式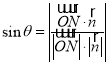 求解.
求解.
(1)因为![]() 是球的直径,则
是球的直径,则![]() ,
,
又![]() 平面
平面![]() ,
,
∴![]() ,
,![]() .∴
.∴![]() 平面
平面![]() ,
,
∴![]() ,∴
,∴![]() 平面
平面![]() .
.
根据证明可知,四面体![]() 是鳖臑.
是鳖臑.
它的每个面的直角分别是![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)如图,
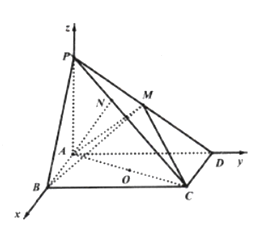
以A为原点,![]() ,
,![]() ,
,![]() 所在直线为x,y,z轴建立直角坐标系,
所在直线为x,y,z轴建立直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,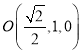 .
.
M为![]() 中点,从而
中点,从而![]() .
.
所以![]() ,设
,设![]() ,
,
则![]() .
.
由![]() ,
,
得![]() .
.
由![]() 得
得![]() ,即
,即![]() .
.
所以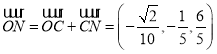 .
.
设平面![]() 的一个法向量为
的一个法向量为![]() .
.
由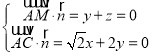 .
.
取![]() ,
,![]() ,
,![]() ,得到
,得到![]() .
.
记![]() 与平面
与平面![]() 所成角为θ,
所成角为θ,
则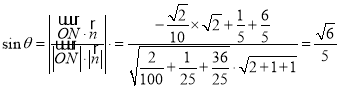 .
.
所以直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目