题目内容
【题目】某厂拟生产甲、乙两种适销产品,每件产品甲的销售收入为3千元,每件产品乙的销售收入为4千元.这两种产品都需要在A,B两种不同的设备上加工,按工艺规定,一件产品甲和一件产品乙在各设备上需要加工工时如表所示:
设备 | A | B |
甲 | 2h | 1h |
乙 | 2h | 2h |
已知A,B两种设备每月有效使用台时数分别为400h、300h(一台设备工作一小时称为一台时).分别用x,y表示计划每月生产甲、乙产品的件数.
(Ⅰ)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问每月分别生产甲、乙两种产品各多少件,可使每月的收入最大?并求出此最大收入.
【答案】解:(Ⅰ)由题意,x,y所满足的数学关系式为  ,
,
画出可行域如图:
(Ⅱ)设每月的销售收入为z千元,则z=3x+4y.
联立 ![]() ,解得B(100,100).
,解得B(100,100).
化目标函数z=3x+4y为y=﹣ ![]() .
.
由图可知,当直线y=﹣ ![]() 过B时,直线在y轴上的截距最大,z有最大值为700.
过B时,直线在y轴上的截距最大,z有最大值为700.
∴每月分别生产甲、乙两种产品分别为100件、100件时,可使每月的收入最大,最大收入为70万元.
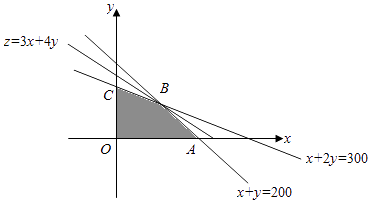
【解析】(1)根据题意,由不等式组在平面直角坐标系中作出可行域,(2)设每月的销售收入为z千元,则z=3x+4y,移动目标函数找到最大值.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
