题目内容
【题目】下列命题:(1)若![]() ,
,![]() 为非零向量且
为非零向量且![]() ,则
,则![]() ;(2)已知向量
;(2)已知向量![]() ,
,![]() ,若
,若![]() ,则
,则![]() ;(3)若
;(3)若![]() ,
,![]() ,
,![]() 为单位向量,且
为单位向量,且![]() ,则三角形
,则三角形![]() 为等边三角形;其中正确的个数是( )
为等边三角形;其中正确的个数是( )
A.1B.2C.3D.0
【答案】B
【解析】
根据平面向量数量积的运算律,可判断(1);由平面向量垂直的坐标运算,可判断(2);根据平面向量数量积的定义,结合夹角求法,即可判断(3).
对于(1),当![]() ,
,![]() 为非零向量且
为非零向量且![]() .由垂直的向量关系可知
.由垂直的向量关系可知![]() ,即
,即![]() ,则
,则![]() ,所以
,所以![]() .故(1)正确.
.故(1)正确.
对于(2),向量![]() ,
,![]() ,若
,若![]() ,则由向量垂直的向量关系可知
,则由向量垂直的向量关系可知![]() .根据向量垂直的坐标运算,可得
.根据向量垂直的坐标运算,可得![]() ,代入化简可得
,代入化简可得![]() ,则
,则![]() ,所以(2)错误.
,所以(2)错误.
对于(3),![]() ,
,![]() ,
,![]() 为单位向量,则
为单位向量,则![]() .由
.由![]() ,可得
,可得
![]() ,两边同时平方展开化简可得
,两边同时平方展开化简可得![]() .
.
由平面向量数量积及![]() 可得
可得![]() .可得
.可得![]() .所以
.所以![]() .由
.由![]() 可得
可得![]() .
.
同理可得![]() ,
,![]() .
.
所以![]() ,即三角形
,即三角形![]() 为等边三角形,所以(3)正确.
为等边三角形,所以(3)正确.
综上可知,正确的为(1),(3)
故选:B

【题目】某一电视台对年龄高于40岁和不高于40岁的人是否喜欢西班牙队进行调查,40岁以上调查了50人,不高于40岁调查了50人,所得数据制成如下列联表:
不喜欢西班牙队 | 喜欢西班牙队 | 总计 | |
40岁以上 |
|
| 50 |
不高于40岁 | 15 | 35 | 50 |
总计 |
|
| 100 |
已知工作人员从所有统计结果中任取一个,取到喜欢西班牙队的人的概率为![]() ,则有超过________的把握认为年龄与西班牙队的被喜欢程度有关.
,则有超过________的把握认为年龄与西班牙队的被喜欢程度有关.
参考公式与临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.702 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每本单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 |
|
|
|
|
|
销量 |
|
|
|
|
|
(1)已知销量![]() 与单价
与单价![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于的线性回归方程;
(2)若该书每本的成本为![]() 元,要使得售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
元,要使得售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: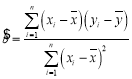
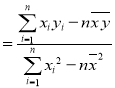 ,
,![]() .
.

