题目内容
17.已知正三棱锥P-ABC中,M,N分别是AB,AP的中点,若MN⊥CN,则此正三棱锥的侧面积与底面ABC的面积之比为$\sqrt{3}$.分析 根据题意,画出图形,结合图形,设出正三棱锥P-ABC的底面边长为a,侧棱长为b,
利用边角关系求出a、b的关系,计算三棱锥的侧面积与底面ABC的面积之比.
解答 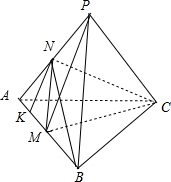 解:根据题意,画出图形,如图所示;
解:根据题意,画出图形,如图所示;
正三棱锥P-ABC中,M、N分别是AB和AP的中点,
且MN⊥CN,
连接CM、BN,过点N作NK⊥AB,垂足为K;
设AB=a,PA=b,
则MN=$\frac{1}{2}$PB=$\frac{1}{2}$b,
MC=$\frac{\sqrt{3}}{2}$AB=$\frac{\sqrt{3}}{2}$a;
∴NC2=MC2-MN2=$\frac{3}{4}$a2-$\frac{1}{4}$b2,
NK=$\frac{1}{2}$PM=$\frac{1}{2}$$\sqrt{{PA}^{2}-{AM}^{2}}$=$\frac{1}{2}$$\sqrt{{b}^{2}-(\frac{a}{2})^{2}}$,
BK=$\frac{3}{4}$AB=$\frac{3}{4}$a;
∴BN2=NK2+BK2=$\frac{1}{4}$(b2-$\frac{1}{4}$a2)+$\frac{9}{16}$a2=$\frac{1}{2}$a2+$\frac{1}{4}$b2,
∴$\frac{3}{4}$a2-$\frac{1}{4}$b2=$\frac{1}{2}$a2+$\frac{1}{4}$b2,
化简得b2=$\frac{1}{2}$a2;
∴$\frac{{S}_{侧面积}}{{S}_{底面积}}$=$\frac{3{S}_{△PAB}}{{S}_{△ABC}}$
=$\frac{3×\frac{1}{2}•AB•PM}{\frac{1}{2}•AB•MC}$=3×$\frac{PM}{MC}$
=3×$\frac{\sqrt{{b}^{2}-{(\frac{a}{2})}^{2}}}{\frac{\sqrt{3}}{2}a}$=$\sqrt{3}$;
即此正三棱锥的侧面积与底面ABC的面积之比为$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了空间中的平行与垂直关系的应用问题,也考查了求三棱锥的侧面积与底面积的应用问题,考查了计算能力与逻辑推理能力,是综合性题目.

 英才计划期末调研系列答案
英才计划期末调研系列答案 在四棱锥P-ABCD中,底面ABCD是梯形,BC∥AD,AD=2BC,AC交BD于点O,试问在棱PA上是否存在点E,使得直线PC∥平面EBD?若存在,求PE:PA的值,并证明你的结论.若不存在,请说明理由.
在四棱锥P-ABCD中,底面ABCD是梯形,BC∥AD,AD=2BC,AC交BD于点O,试问在棱PA上是否存在点E,使得直线PC∥平面EBD?若存在,求PE:PA的值,并证明你的结论.若不存在,请说明理由.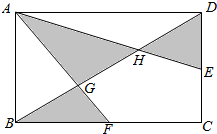 如图:长方体ABCD中,AB=10厘米,BC=15厘米,E,F分别是所在边的中点,求阴影部分的面积.(提示:由于图中AD平行于BC,可知AD:BF=AG:CF=DG:BG)
如图:长方体ABCD中,AB=10厘米,BC=15厘米,E,F分别是所在边的中点,求阴影部分的面积.(提示:由于图中AD平行于BC,可知AD:BF=AG:CF=DG:BG)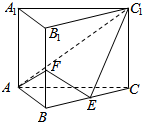 已知在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=2,E,F分别是BC,BB1的中点.
已知在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=2,E,F分别是BC,BB1的中点.