题目内容
7.在坐标平面内,对任意非零实数m,不在抛物线y=mx2+(2m+1)x-(3m+2)上且在直线y=-x+1上的点的坐标为(1,0),(-3,4),($\frac{3}{2}$,-$\frac{1}{2}$).分析 设(s,t)在直线y=1-x上,即有t=1-s,代入抛物线方程,可得m(s2+2s-3)+(2s-3)≠0(m≠0)恒成立,由恒成立思想即可得到s的值,进而得到所求点.
解答 解:设(s,t)在直线y=1-x上,即有t=1-s,
由题意可得1-s≠ms2+(2m+1)s-(3m+2),
即为m(s2+2s-3)+(2s-3)≠0(m≠0)恒成立,
即有s2+2s-3=0或2s-3=0,
解得s=1或-3或$\frac{3}{2}$,
则所求点为(1,0),(-3,4),($\frac{3}{2}$,-$\frac{1}{2}$).
故答案为:(1,0),(-3,4),($\frac{3}{2}$,-$\frac{1}{2}$).
点评 本题考查抛物线的方程和应用,考查直线和抛物线的位置关系,以及恒成立思想的运用,属于中档题.

练习册系列答案
相关题目
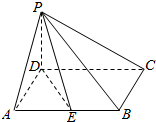 已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,点E为AB中点.
已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,点E为AB中点.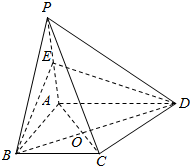 在四棱锥P-ABCD中,底面ABCD是梯形,BC∥AD,AD=2BC,AC交BD于点O,试问在棱PA上是否存在点E,使得直线PC∥平面EBD?若存在,求PE:PA的值,并证明你的结论.若不存在,请说明理由.
在四棱锥P-ABCD中,底面ABCD是梯形,BC∥AD,AD=2BC,AC交BD于点O,试问在棱PA上是否存在点E,使得直线PC∥平面EBD?若存在,求PE:PA的值,并证明你的结论.若不存在,请说明理由.