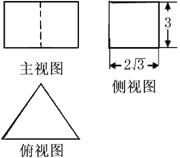
题目内容
四棱锥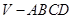
中，底面
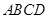是边长为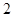
的正方形，其他四个侧面都是侧棱长为
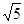的等腰三角形，则二面角
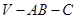的平面角为_____________。翰林汇
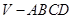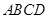中，底面是边长为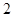的正方形，其他四个侧面都是侧棱长为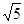的等腰三角形，则二面角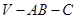的平面角为_____________。翰林汇60°
取AB、CD的中点E、F，连接VE、EF、VF
∵VA=VB=
∴△VAB为等腰三角形
∴VE⊥AB又∵ABCD是正方形，则BC⊥AB
∵EF∥BC∴EF⊥AB∵EF∩VE=E∴∠VEF为二面角V-AB-C的平面角
∵△VAB≌△VDC∴VE=VF=2EF=BC=2∴△VEF为等边三角形
∴∠VEF=60°即二面角V-AB-C为60°
故答案为：60°
∵VA=VB=
∴△VAB为等腰三角形∴VE⊥AB又∵ABCD是正方形，则BC⊥AB
∵EF∥BC∴EF⊥AB∵EF∩VE=E∴∠VEF为二面角V-AB-C的平面角
∵△VAB≌△VDC∴VE=VF=2EF=BC=2∴△VEF为等边三角形
∴∠VEF=60°即二面角V-AB-C为60°
故答案为：60°
练习册系列答案
相关题目
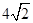
,SA=SC=2,，二面角S—AC—B的余弦值是
，若S、A、B、C都在同一球面上，则该球的表面积是
B．
C．24
D．6
内有一个球与正方体的各个面都相切，经过
和
作一个截面，正确的截面图是 .
