题目内容
在三棱锥S—ABC中,AB⊥BC,AB=BC= ,SA=SC=2,,二面角S—AC—B的余弦值是
,SA=SC=2,,二面角S—AC—B的余弦值是 ,若S、A、B、C都在同一球面上,则该球的表面积是
,若S、A、B、C都在同一球面上,则该球的表面积是
A. B.
B. C.24
C.24 D.6
D.6
 ,SA=SC=2,,二面角S—AC—B的余弦值是
,SA=SC=2,,二面角S—AC—B的余弦值是 ,若S、A、B、C都在同一球面上,则该球的表面积是
,若S、A、B、C都在同一球面上,则该球的表面积是A.
 B.
B. C.24
C.24 D.6
D.6
D
因为由AB⊥BC,得△ABC的外接圆的圆心O′为AC中点,连接SO′,BO′,由SA=SC和AB=BC有SO′⊥AC,BO′⊥AC
而四面体外接球的球心O在平面SO′B内,连接OO′,有OO′⊥底面ABC
将平面SO′B取出,则BO′=1,SO′=

用余弦定理可得cos∠SO′B=-
∴SB=
作SB的中垂线,过O′作BO′的垂线,两者必相交于O,用余弦定理,cos∠O′BS= 如图,BE=O′B÷cos∠O′BS=
如图,BE=O′B÷cos∠O′BS= =
= 也就是D,E,O三点重合了
也就是D,E,O三点重合了
外接圆的半径R=OB= ∴球的表面积是4πR2=6π
∴球的表面积是4πR2=6π
故选D.
而四面体外接球的球心O在平面SO′B内,连接OO′,有OO′⊥底面ABC
将平面SO′B取出,则BO′=1,SO′=


用余弦定理可得cos∠SO′B=-

∴SB=

作SB的中垂线,过O′作BO′的垂线,两者必相交于O,用余弦定理,cos∠O′BS=
 如图,BE=O′B÷cos∠O′BS=
如图,BE=O′B÷cos∠O′BS= =
= 也就是D,E,O三点重合了
也就是D,E,O三点重合了外接圆的半径R=OB=
 ∴球的表面积是4πR2=6π
∴球的表面积是4πR2=6π故选D.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
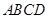 满足
满足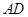 ∥
∥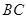 ,
,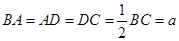 ,
,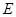 是
是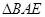 沿着
沿着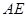 翻折成
翻折成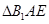 ,使面
,使面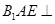 面
面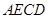 ,
,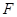 为
为 的中点.
的中点. 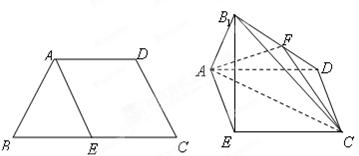
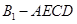 的体积;(Ⅱ)证明:
的体积;(Ⅱ)证明: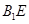 ∥面
∥面 ;
;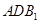 与面
与面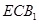 所成二面角的余弦值.
所成二面角的余弦值.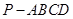 中,平面
中,平面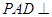 平面
平面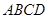 ,
,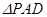 为等边三角形,底面
为等边三角形,底面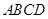 为菱形,
为菱形,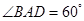 ,
,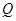 为
为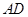 的中点,
的中点,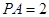 。
。
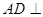 平面
平面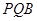 ;
;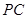 上是否存在点
上是否存在点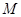 ,使
,使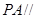 平面
平面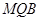 ; 若存在,求出
; 若存在,求出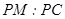 的值。
的值。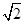 。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E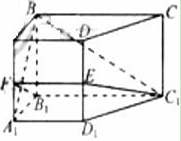



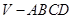 中,底面
中,底面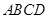 是边长为
是边长为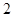 的正方形,其他四个侧面都是侧棱长为
的正方形,其他四个侧面都是侧棱长为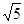 的等腰三角形,则二面角
的等腰三角形,则二面角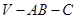 的平面角为_____________。翰林汇
的平面角为_____________。翰林汇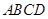 中,
中,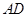 ∥
∥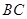 ,
,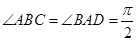 ,
,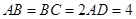 ,
,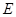 、
、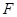 分别是
分别是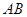 、
、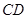 上的点,
上的点,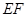 ∥
∥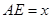 ,
, 是
是 ⊥平面
⊥平面 (如图).
(如图).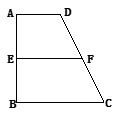
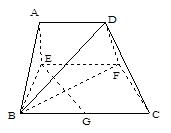
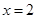 时,求证:
时,求证: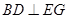 ;
;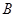 、
、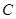 、
、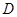 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为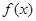 ,求
,求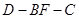 的余弦值.
的余弦值.