题目内容
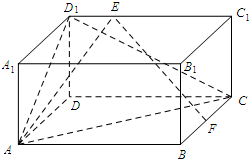 如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=2,A1A=2,点F是棱BC的中点,点E在棱C1D1上,且D1E=λEC1(λ为实数).
如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=2,A1A=2,点F是棱BC的中点,点E在棱C1D1上,且D1E=λEC1(λ为实数).(1)求二面角D1-AC-D的余弦值;
(2)当λ=
| 1 | 3 |
(3)求证:直线EF与直线EA不可能垂直.
分析:(1)建立如图所示空间直角坐标系,算出向量
、
的坐标,利用垂直向量数量积为0的方法建立方程组,算出平面D1AC的一个法向量
=(2,1,2),结合平面DAC的一个法向量为
=(0,0,1)最后用空间向量的夹角公式即可算出二面角D1-AC-D的余弦值;
(2)当λ=
时,可得E、F的坐标,从而
=(1,3,-2),进而算出<
,
>的余弦值,再由<
,
>为锐角,结合直线与平面所成角的定义,即可算出直线EF与平面D1AC所成角的正弦值的大小;
(3)假设EF⊥EA,由
•
=0建立关于λ的等式,化简可得3λ2-2λ+3=0,由根的判别式得该方程无解,所以原假设不成立,从而得到直线EF不可能与直线EA不可能垂直.
| D1A |
| D1C |
| n |
| m |
(2)当λ=
| 1 |
| 3 |
| EF |
| EF |
| n |
| EF |
| n |
(3)假设EF⊥EA,由
| EF |
| EA |
解答:解:(1)以DA、DC、DD1为x、y、z轴,建立空间直角坐标系D-xyz,如图所示.
则A(2,0,0),C(0,4,0),D1(0,0,2),
=(2,0,-2),
=(0,4,-2). …(2分)
设平面D1AC的法向量为
=(x,y,z),
则
•
=0,
•
=0.
即x=z,z=2y.令y=1,则x=z=2.
∴平面D1AC的一个法向量
=(2,1,2).…(4分)
又平面DAC的一个法向量为
=(0,0,1).
故cos<
,
>=
=
=
,
即二面角D1-AC-D的余弦值为
. …(6分)
(2)当λ=
时,E(0,1,2),F(1,4,0),
=(1,3,-2).
所以cos <
,
>=
=
=
. …(9分)
因为 cos<
,
>>0,所以<
,
>为锐角,
从而直线EF与平面D1AC所成角的正弦值的大小为
. …(10分)
(3)假设EF⊥EA,则
•
=0.
∵E(0,
,2),F(1,4,0),
∴
=(2,-
,-2),
=(1,4-
,-2). …(12分)
∴2-
(4-
)+4=0.化简得3λ2-2λ+3=0.
该方程无解,所以假设不成立,即直线EF不可能与直线EA不可能垂直.…(14分)

则A(2,0,0),C(0,4,0),D1(0,0,2),
| D1A |
| D1C |
设平面D1AC的法向量为
| n |
则
| n |
| D1A |
| n |
| D1C |
即x=z,z=2y.令y=1,则x=z=2.
∴平面D1AC的一个法向量
| n |
又平面DAC的一个法向量为
| m |
故cos<
| m |
| n |
| ||||
|
|
| 2 |
| 1×3 |
| 2 |
| 3 |
即二面角D1-AC-D的余弦值为
| 2 |
| 3 |
(2)当λ=
| 1 |
| 3 |
| EF |
所以cos <
| EF |
| n |
| ||||
|
|
| 1 | ||
|
| ||
| 42 |
因为 cos<
| EF |
| n |
| EF |
| n |
从而直线EF与平面D1AC所成角的正弦值的大小为
| ||
| 42 |
(3)假设EF⊥EA,则
| EF |
| EA |
∵E(0,
| 4λ |
| 1+λ |
∴
| EA |
| 4λ |
| 1+λ |
| EF |
| 4λ |
| 1+λ |
∴2-
| 4λ |
| 1+λ |
| 4λ |
| 1+λ |
该方程无解,所以假设不成立,即直线EF不可能与直线EA不可能垂直.…(14分)
点评:本题给出长方体模型,求二面角的余弦值和线面角的正弦值,并探索线线垂直的问题.着重考查了长方体的性质、利用空间向量研究线面角与面面角等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为:
如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为: 如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )
如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )

 .
. 
 ,AA1 =
,AA1 = ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.