题目内容
已知实数x,y满足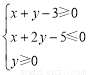 ,则
,则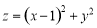 的最小值是 .
的最小值是 .
2
【解析】
试题分析:线性不等式组表示的可行域如图:
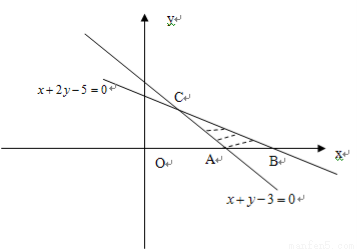
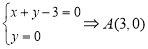 ,
,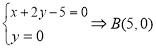 ,
,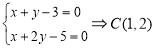 。
。
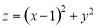 表示点
表示点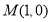 与可行域内的点间的距离的平方。
与可行域内的点间的距离的平方。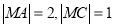 ,点
,点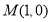 到直线
到直线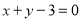 的距离为
的距离为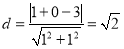 ,因为
,因为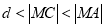 ,所以
,所以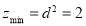 。
。
考点:线性规划。

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
题目内容
已知实数x,y满足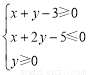 ,则
,则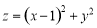 的最小值是 .
的最小值是 .
2
【解析】
试题分析:线性不等式组表示的可行域如图:

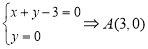 ,
,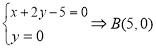 ,
,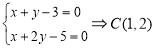 。
。
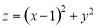 表示点
表示点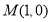 与可行域内的点间的距离的平方。
与可行域内的点间的距离的平方。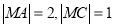 ,点
,点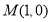 到直线
到直线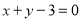 的距离为
的距离为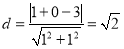 ,因为
,因为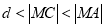 ,所以
,所以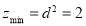 。
。
考点:线性规划。

 53天天练系列答案
53天天练系列答案