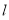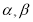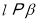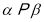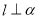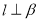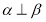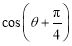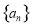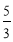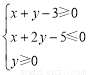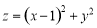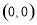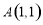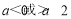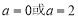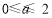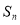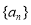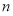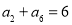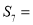题目内容
已知函数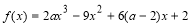 ,
,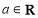 .
.
(1)若函数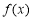 在
在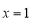 处取得极值,求实数
处取得极值,求实数 的值;
的值;
(2)若 ,求函数
,求函数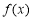 在区间
在区间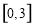 上的最大值和最小值.
上的最大值和最小值.
(1)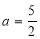 (2)最小值
(2)最小值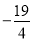 ,最大值29
,最大值29
【解析】
试题分析:(1)先求导,因为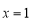 是函数
是函数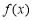 的极值点,则
的极值点,则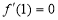 ,即可求实数
,即可求实数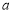 的值。(2)先求导再令导数等于0,导论导数的正负得函数的增减区间,根据函数的增减性可求其最值。
的值。(2)先求导再令导数等于0,导论导数的正负得函数的增减区间,根据函数的增减性可求其最值。
试题解析:解答:(1)∵函数 ,
,
∴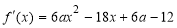 . 2分
. 2分
∵函数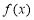 在
在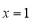 处取得极值,∴
处取得极值,∴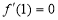 ,
,
∴ ,∴实数
,∴实数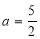 . 4分
. 4分
经检验,当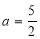 时,
时,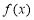 取得极小值,故
取得极小值,故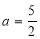 . 6分
. 6分
(2)当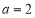 时,
时,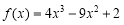 .
.
∵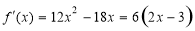 ,∴
,∴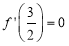 . 8分
. 8分
∵在区间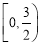 上,
上,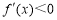 ;在区间
;在区间 上,
上,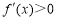 ,
,
∴在区间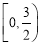 上,函数
上,函数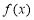 单调递减;在区间
单调递减;在区间 上,函数
上,函数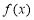 单调递增.10分
单调递增.10分
∴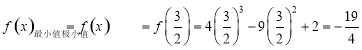 . 11分
. 11分
∵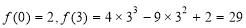 ,∴
,∴ . 12分
. 12分
考点:1导数;2用导数研究函数的单调性。

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目