题目内容
1. 如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是$\frac{\sqrt{2}}{6}$.
如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是$\frac{\sqrt{2}}{6}$.
分析 根据展开图的特征可知该多面体为正四棱锥,底面边长为1,侧棱长为1,斜高为$\frac{\sqrt{3}}{2}$,连接顶点和底面中心即为高,最后用棱锥的体积公式求解.
解答  解:由题知该多面体为正四棱锥,如图所示:
解:由题知该多面体为正四棱锥,如图所示:
底面边长为1,侧棱长为1,斜高为SE=$\frac{\sqrt{3}}{2}$,
连接顶点和底面中心即为高,
可求高为SO=$\frac{\sqrt{2}}{2}$,
所以体积为V=$\frac{1}{3}$•1•1•$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{6}$.
故答案为:$\frac{{\sqrt{2}}}{6}$.
点评 本题主要考查正四棱锥的结构特征及棱,高,斜高的求法,同时,还考查了平面图形与空间图形间的转化能力和求解几何体大小的运算能力,属中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
6.正方体的棱长为1,C、D、M分别为三条棱的中点,A、B是顶点,那么点M到截面ABCD的距离是( ) 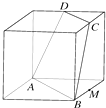

| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{2}$ |
 如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AC=BC,AB=2A1A=4.以AB,BC为邻边作平行四边形ABCD,连接A1D和DC1.
如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AC=BC,AB=2A1A=4.以AB,BC为邻边作平行四边形ABCD,连接A1D和DC1. 如图,将边长为2的正方形ABCD沿对角线BD对折,使得平面BCD⊥平面ABD,点E是BD中点,点F满足:FA∥CE,且FA=2$\sqrt{2}$.
如图,将边长为2的正方形ABCD沿对角线BD对折,使得平面BCD⊥平面ABD,点E是BD中点,点F满足:FA∥CE,且FA=2$\sqrt{2}$.