题目内容
2.已知cos($\frac{π}{4}$+α)=$\frac{5}{13}$,cos($\frac{π}{4}$-β)=$\frac{3}{5}$,α∈(-$\frac{π}{4}$,$\frac{π}{4}$),β∈($\frac{π}{4}$,$\frac{3π}{4}$).(1)求sinα的值;
(2)求cos(α-β)的值.
分析 (1)由两角和与差的余弦函数公式化简已知可得$cosα=\frac{5\sqrt{2}}{13}+sinα$,结合α的范围,两边平方整理可得:338sin2α+130$\sqrt{2}$sinα-119=0,即可解得sinα的值.
(2)由已知可求$\frac{π}{4}$+α∈(0,$\frac{π}{2}$),$\frac{π}{4}$-β∈(-$\frac{π}{2}$,0),从而可求sin($\frac{π}{4}$+α),sin($\frac{π}{4}$-β),由cos(α-β)=sin[($\frac{π}{4}$+α)+($\frac{π}{4}$-β)]即可求值.
解答 解:(1)∵cos($\frac{π}{4}$+α)=$\frac{5}{13}$,
∴化简可得:cos$α-sinα=\frac{5\sqrt{2}}{13}$,既有:$cosα=\frac{5\sqrt{2}}{13}+sinα$,
∵α∈(-$\frac{π}{4}$,$\frac{π}{4}$),cosα>0,
∴两边平方整理可得:338sin2α+130$\sqrt{2}$sinα-119=0,
∴解得:sinα=$\frac{-130\sqrt{2}±312\sqrt{2}}{676}$=$\frac{91\sqrt{2}}{338}$或-$\frac{221\sqrt{2}}{338}$.
(2)∵α∈(-$\frac{π}{4}$,$\frac{π}{4}$),β∈($\frac{π}{4}$,$\frac{3π}{4}$).
∴$\frac{π}{4}$+α∈(0,$\frac{π}{2}$),$\frac{π}{4}$-β∈(-$\frac{π}{2}$,0),
∴sin($\frac{π}{4}$+α)=$\sqrt{1-co{s}^{2}(\frac{π}{4}+α)}$=$\frac{12}{13}$,sin($\frac{π}{4}$-β)=-$\sqrt{1-co{s}^{2}(\frac{π}{4}-β)}$=-$\frac{4}{5}$,
cos(α-β)=sin[$\frac{π}{2}$+(α-β)]
=sin[($\frac{π}{4}$+α)+($\frac{π}{4}$-β)]
=sin($\frac{π}{4}$+α)cos($\frac{π}{4}$-β)+cos($\frac{π}{4}$+α)sin($\frac{π}{4}$-β)
=$\frac{12}{13}×\frac{3}{5}+\frac{5}{13}×(-\frac{4}{5})$
=$\frac{16}{65}$.
点评 本题主要考查了两角和与差的余弦函数公式,两角和与差的正弦函数公式,同角三角函数关系式的应用,考查了计算能力,属于基本知识的考查.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | ∅ | B. | [-2,2] | C. | [2,+∞) | D. | R |
| A. | 3<m<6 | B. | 1<m<3 | C. | 0<m<1 | D. | -1<m<0 |
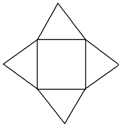 如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是$\frac{\sqrt{2}}{6}$.
如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是$\frac{\sqrt{2}}{6}$.