题目内容
13.幂函数f(x)=xα(α为常数)的图象经过点($\frac{1}{2},\frac{1}{4}$)(1)求函数f(x)的解析式;
(2)x∈[-1,1]时,函数y=f(x)-2ax+3的最小值为g(a),求g(a)的表达式;
(3)是否存在实数m>n>0,使得a∈[n,m]时,总有g(a)∈[n2,m2]成立,若存在,求出m,n的值,否则说明理由.
分析 (1)根据幂函数的定义,利用待定系数法即可得到结论..
(2)给出的函数是二次函数,求出其对称轴方程,分对称轴在给定的区间左侧,右侧及在区间内,利用函数的单调性求出其在不同区间内的最小值,即可.
(3)根据(2)中g(a)的表达式,作出对应的图象,利用函数的单调性,分别进行讨论判断即可.
解答 解:(1)∵幂函数f(x)=xα(α为常数)的图象经过点($\frac{1}{2},\frac{1}{4}$)
∴f($\frac{1}{2}$)=$(\frac{1}{2})^{α}=\frac{1}{4}$,则α=2,即f(x)=x2.
(2)若x∈[-1,1]时,函数y=f(x)-2ax+3=x2-2ax+3=(x-a)2+3-a2,
对称轴为x=a,
①若a>1,则函数在[-1,1]上为减函数,则函数的最小值为g(a)=f(1)=4-2a,
②若-1≤a≤1,则函数的最小值为g(a)=f(a)=3-a2,
③若a<-1,则函数在[-1,1]上为增函数,则函数的最小值为g(a)=f(-1)=4+2a.
(3)由(1)知g(a)=$\left\{\begin{array}{l}{4-2a,}&{a>1}\\{3-{a}^{2},}&{-1≤a≤1}\\{4+2a,}&{a<-1}\end{array}\right.$,
∵m>n>0,
∴作出函数g(a)在(0,+∞)上的图象,则函数g(a)为减函数,
①若0<n<m≤1,则由g(a)∈[n2,m2]成立,
得$\left\{\begin{array}{l}{3-{n}^{2}={m}^{2}}\\{3-{m}^{2}={n}^{2}}\end{array}\right.$,
∵3-n2>1,m2<1,此时方程3-n2=m2不成立.
②若1≤n<m,则由g(a)∈[n2,m2]成立,
得$\left\{\begin{array}{l}{4-2m={n}^{2}}\\{4-2n={m}^{2}}\end{array}\right.$,两式作差得2(n-m)=n2-m2=(n-m)(n+m),
即n+m=2,
∵1≤n<m,∴n+m>2,此时此时方程n+m=2不成立.
③0<n≤1≤m,(等号不同时取),
则由g(a)∈[n2,m2]成立,
得$\left\{\begin{array}{l}{3-{n}^{2}={m}^{2}}\\{4-2m={n}^{2}}\end{array}\right.$,消去n得(m-1)2=0,
则m=1,此时n2=4-2=2,则n=$\sqrt{2}$>1,不成立,
综上不存在实数m>n>0,使得a∈[n,m]时,总有g(a)∈[n2,m2]成立.
点评 本题考查了二次函数的性质,考查了分类讨论求二次函数在不同区间上的最值,须注意的是分段函数的值域要分段求,综合性较强,有一定的难度.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
| A. | {1,5,6} | B. | {1,4,5,6} | C. | {2,3,4} | D. | {1,6} |
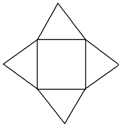 如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是$\frac{\sqrt{2}}{6}$.
如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是$\frac{\sqrt{2}}{6}$.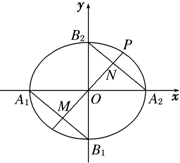 如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的左、右顶点分别是A1,A2,上、下顶点分别为B2,B1,点P($\frac{3}{5}$a,m)(m>0)是椭圆C上一点,PO⊥A2B2,直线PO分别交A1B1,A2B2于点M,N.
如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的左、右顶点分别是A1,A2,上、下顶点分别为B2,B1,点P($\frac{3}{5}$a,m)(m>0)是椭圆C上一点,PO⊥A2B2,直线PO分别交A1B1,A2B2于点M,N.