题目内容
13．若实数x，y满足不等式组$\left\{\begin{array}{l}{y≥2x-1}\\{y≤x+1}\end{array}\right.$，则z=x+3y的最大值是（ ）| A． | -3 | B． | $\frac{1}{3}$ | C． | 11 | D． | 9 |
分析 作出不等式组对于的平面区域，利用数形结合即可得到结论．
解答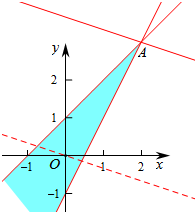 
解：作出不等式组对于的平面区域如图：
由z=x+3y，则y=$-\frac{1}{3}x$$+\frac{z}{3}$，
平移直线y=$-\frac{1}{3}x$$+\frac{z}{3}$，
由图象可知当直线y=$-\frac{1}{3}x$$+\frac{z}{3}$经过点A时，直线y=$-\frac{1}{3}x$$+\frac{z}{3}$的截距最大，此时z最大，
由$\left\{\begin{array}{l}{y=2x-1}\\{y=x+1}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$，
即A（2，3），
此时zmax=2+3×3=11，
故选：C．
点评 本题主要考查线性规划的应用，利用z的几何意义，利用数形结合是解决本题的关键．
练习册系列答案
字词句段篇系列答案
相关题目
8．设正实数a，b满足a+2b=ab，则a+b的最小值为（ ）
| A． | $\sqrt{2}$ | B． | 4$\sqrt{2}$ | C． | 3+2$\sqrt{2}$ | D． | 6 |
设抛物线C：y2=x与直线l交于A，B两点（异于原点O），以AB为直径的圆恰好经过原点O．
5．随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明，得到如下2×2列联表：
（1）根据以上列联表进行独立性检验，能否在犯错误的概率不超过0.01的前提下认为“性别与是否读营养说明之间有关系”？
（2）从被询问的16名不读营养说明的大学生中，随机抽取2名学生，求抽到男生人数ξ的分布列及其数学期望．
| 读营养说明 | 不读营养说明 | 合计 | |
| 男 | 16 | 4 | 20 |
| 女 | 8 | 12 | 20 |
| 合计 | 24 | 16 | 40 |
（2）从被询问的16名不读营养说明的大学生中，随机抽取2名学生，求抽到男生人数ξ的分布列及其数学期望．
2．校本课程是由学校自主开发的课程，与必修课程一起构成学校课程体系．某校开设校本课程“数学史选讲”，为了了解该课程学生的喜好程度是否跟性别有关，随机调查了50名同学，结果如下：25名男生中有10名喜欢，15名不喜欢；25名女生中有20名喜欢，5名不喜欢．
（Ⅰ）根据以上数据完成2×2列联表
（Ⅱ）有多大的把握认为该课程的喜好程度与学生的性别有关？（参考公式与数值附后）
参考公式与数值：K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
（Ⅰ）根据以上数据完成2×2列联表
| 性别 喜好 | 男 | 女 | 合计 |
| 喜欢 | 10 | 20 | 30 |
| 不喜欢 | 15 | 5 | 20 |
| 合计 | 25 | 25 | 50 |
参考公式与数值：K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
| P（K2≥k） | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
