题目内容
4.观察下列等式: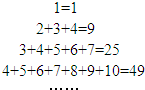
照以上式子规律:
(1)写出第5个等式,并猜想第n个等式; (n∈N*)
(2)用数学归纳法证明上述所猜想的第n个等式成立.(n∈N*)
分析 (1)通过前4个表达式,直接写出第5个等式,并猜想第n个等式;(n∈N*)
(2)用数学归纳法证明步骤,直接证明上述所猜想的第n个等式成立.(n∈N*)
解答 解:(1)第5个等式为:5+6+7+8+9+10+11+12+13=92…(2分)
第n个等式为:n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2,n∈N*…(5分)
(2)①当n=1时,等式左边=1,等式右边=(2-1)2=1,所以等式成立.…(6分)
②假设n=k(k∈N*)时,等式成立,即k+(k+1)+(k+2)+…+(3k-2)=(2k-1)2(k≥1,k∈N*)
那么,当n=k+1时,(k+1)+(k+2)+(k+3)+…+(3k+1)=k+(k+1)+(k+2)+…+(3k-2)+(3k-1)+3k+(3k+1)-k=(2k-1)2+8k=[2(k+1)-1)2,
即n=k+1时等式成立.…(11分)
根据(1)和(2),可知对任何n∈N*,等式都成立.…(12分)
点评 本题考查数学归纳法证明猜想成立,注意证明步骤的应用,缺一不可.

练习册系列答案
相关题目
13.若实数x,y满足不等式组$\left\{\begin{array}{l}{y≥2x-1}\\{y≤x+1}\end{array}\right.$,则z=x+3y的最大值是( )
| A. | -3 | B. | $\frac{1}{3}$ | C. | 11 | D. | 9 |
14.一位母亲记录了她儿子3周岁到9周岁的身高,建立了她儿子身高y与年龄x的回归模型$\widehat{y}$=73.93+7.19x,她用这个模型预测她儿子10周岁时的身高,则下面的叙述正确的是( )
| A. | 她儿子10周岁时的身高一定是145.83cm | |
| B. | 她儿子10周岁时的身高在145.83cm以上 | |
| C. | 她儿子10周岁时的身高在145.83cm左右 | |
| D. | 她儿子10周岁时的身高在145.83cm以下 |