题目内容
(本题满分14分)已知椭圆C: =1(a>b>0)的离心率为
=1(a>b>0)的离心率为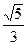 ,短轴一
,短轴一
个端点到右焦点的距离为3.
(1)求椭圆C的方程;
(2)过椭圆C上的动点P引圆O: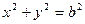 的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.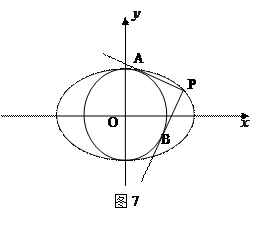
解:(1)设椭圆的半焦距为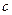 ,依题意
,依题意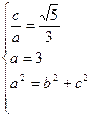 ---------------- 3分
---------------- 3分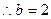 ,------------------------------4分
,------------------------------4分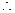 所求椭圆方程为
所求椭圆方程为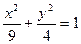 ------------------------------5分
------------------------------5分
(2)如图,设P点坐标为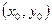 ,--------------------------6分
,--------------------------6分
若 ,则有
,则有 .-----------------------7分
.-----------------------7分
即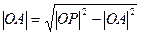 -----------------------------8分
-----------------------------8分
有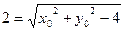
两边平方得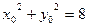 ……①------------------------------9分
……①------------------------------9分
又因为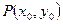 在椭圆上,所以
在椭圆上,所以 ……②------------------------------10分
……②------------------------------10分
①,②联立解得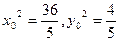 ------------------------------11分
------------------------------11分
所以满足条件的有以下四组解 ,
,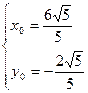 ,
,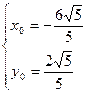 ,
,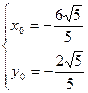 ------------------------------13分
------------------------------13分
所以,椭圆C上存在四个点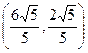 ,
,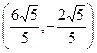 ,
,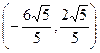 ,
, ,分别由这四个点向圆O所引的两条切线均互相垂直. -----------14分
,分别由这四个点向圆O所引的两条切线均互相垂直. -----------14分
解析

练习册系列答案
相关题目
22.(本题满分15分)已知抛物线C的顶点在原点,焦点在y轴正半轴上,点 到其准线的距离等于5.
到其准线的距离等于5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)如图,过抛物线C的焦点的直线从左到右依次与抛物线C及圆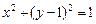 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明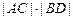 为定值;
为定值;
|
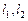 且
且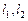 交于点M,求
交于点M,求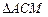 与
与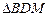 面积之和的最小值.
面积之和的最小值. 直线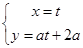 (t为参数)与曲线
(t为参数)与曲线 =1的位置关系是( )
=1的位置关系是( )
| A.相离 | B.相交 | C.相切 | D.不确定 |
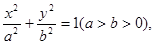 它的一个焦点与抛物线
它的一个焦点与抛物线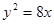 的焦点重合,离心率
的焦点重合,离心率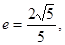 过椭圆的右焦点F作与坐标轴不垂直的直线
过椭圆的右焦点F作与坐标轴不垂直的直线 交椭圆于A、B两点.(Ⅰ)求椭圆的标准方程;
交椭圆于A、B两点.(Ⅰ)求椭圆的标准方程;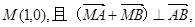 求直线
求直线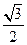 ,求m的值及椭圆的长轴和短轴的长及顶点坐标.
,求m的值及椭圆的长轴和短轴的长及顶点坐标.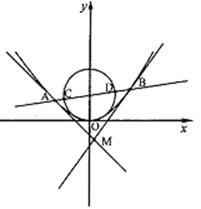
 题满分13分)
题满分13分)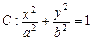 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆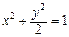 有相同的离心率,斜
有相同的离心率,斜 ),与椭圆C交于不同两点A、B.
),与椭圆C交于不同两点A、B.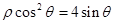 的焦点的极坐标 .
的焦点的极坐标 .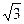 )的直线l过点(0,-2
)的直线l过点(0,-2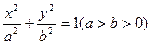
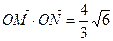 cot∠MON ≠0(O为原点).若存在,求直线m的方程;若不存
cot∠MON ≠0(O为原点).若存在,求直线m的方程;若不存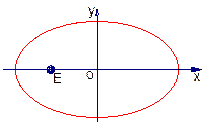
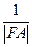 +
+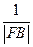 为定值.
为定值.