Question

【题目】已知曲线C：9x2+4y2=36，直线l： （t为参数）

（Ⅰ）写出曲线C的参数方程，直线l的普通方程；

（Ⅱ）过曲线C上任意一点P作与l夹角为30°的直线，交l于点A，求|PA|的最大值与最小值．

Answer 1

【答案】（I） ， （II）|PA|的最大值与最小值分别为

【解析】试题分析：（I）曲线C：9x2+4y2=36，化为 ，利用cos2θ+sin2θ=1可得参数方程．直线l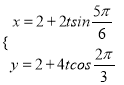： （t为参数），即 ，即可化为普通方程．

（II）点P（2cosθ，3sinθ）到直线l的距离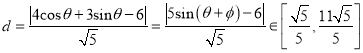 ，利用|PA|==2d即可得出．

试题解析：

（I）曲线C：9x2+4y2=36，化为，可得参数方程： ．

直线l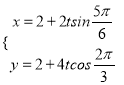： （t为参数），即，化为：2x+y﹣6=0．

（II）点P（2cosθ，3sinθ）到直线l的距离，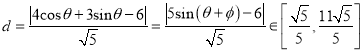

|PA|==2d∈．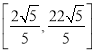

∴|PA|的最大值与最小值分别为．