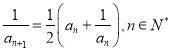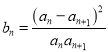题目内容
【题目】对于x∈R,[x]表示不超过x的最整数,如[1.1]=1,[﹣2.1]=﹣3.定义R上的函数f(x)=[2x]+[4x]+[8x],若A={y|y=f(x),0≤x≤ ![]() },则A中所有元素的和为( )
},则A中所有元素的和为( )
A.15
B.19
C.20
D.55
【答案】A
【解析】∵任意x,[x]表示不超过x的最大整数,如[1,1]=1[﹣2,1]=﹣3,定义R上的函数f(x)=[2x]+[4x]+[8x],
若A={y|y=f(x),0≤x≤ ![]() },
},
当 x∈[0, ![]() ),0≤2x<
),0≤2x< ![]() ,0≤4x<
,0≤4x< ![]() ,0≤8x<1,∴f(x)=[2x]+[4x]+[8x]=0
,0≤8x<1,∴f(x)=[2x]+[4x]+[8x]=0
当 x∈[ ![]() ,
, ![]() ),
), ![]() ≤2x<
≤2x< ![]() ,
, ![]() ≤4x<1,1≤8x<2,∴f(x)=[2x]+[4x]+[8x]=0+1=1
≤4x<1,1≤8x<2,∴f(x)=[2x]+[4x]+[8x]=0+1=1
当 x∈[ ![]() ,
, ![]() ),
), ![]() ≤2x<
≤2x< ![]() ,1≤4x<
,1≤4x< ![]() ,2≤8x<3,∴f(x)=[2x]+[4x]+[8x]=0+1+2=3
,2≤8x<3,∴f(x)=[2x]+[4x]+[8x]=0+1+2=3
当 x∈[ ![]() ,
, ![]() ),
), ![]() ≤2x<1,
≤2x<1, ![]() ≤4x<2,3≤8x<4,∴f(x)=[2x]+[4x]+[8x]=0+1+3=4
≤4x<2,3≤8x<4,∴f(x)=[2x]+[4x]+[8x]=0+1+3=4
当 x= ![]() 时,则f(
时,则f( ![]() )=[2×
)=[2× ![]() ]+[4×
]+[4× ![]() ]+[8×
]+[8× ![]() ]=1+2+4=7
]=1+2+4=7
所以A中所有元素的和为0+1+3+4+7=15.
故选A.
【考点精析】利用元素与集合关系的判断对题目进行判断即可得到答案,需要熟知对象![]() 与集合
与集合![]() 的关系是
的关系是![]() ,或者
,或者![]() ,两者必居其一.
,两者必居其一.

练习册系列答案
相关题目