题目内容
【题目】若f(x)=x2﹣x+b,且f(log2a)=b,log2f(a)=2(a>0且a≠1),
(1)求a,b;
(2)求f(log2x)的最小值及相应 x的值;
(3)若f(log2x)>f(1)且log2f(x)<f(1),求x的取值范围.
【答案】
(1)解:∵f (x)=x2﹣x+b,∴f (log2a)=(log2a)2﹣loga+b=b,
∴log2a=1,∴a=2.
又∵log2f(a)=2,f(a)=4.∴a2﹣a+b=4,∴b=2.
(2)解:由(1)得f (x)=x2﹣x+2
∴f (log2x)=(log2x)2﹣log2x+2=(log2x﹣ ![]() )2+
)2+ ![]() ,
,
∴当log2x= ![]() ,即x=
,即x= ![]() 时,f (log2x)有最小值
时,f (log2x)有最小值 ![]() .
.
(3)解:由题意知: 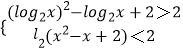 ,
,
解得 ![]() ,
,
∴ ![]() ,
,
∴0<x<1
【解析】(1)代入利用对数的运算性质即可得出.(2)利用二次函数与对数函数的单调性即可得出.(3)由题意知: 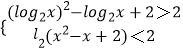 ,利用一元二次不等式的解法、对数函数的单调性即可得出.
,利用一元二次不等式的解法、对数函数的单调性即可得出.
【考点精析】根据题目的已知条件,利用二次函数的性质和对数的运算性质的相关知识可以得到问题的答案,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减;①加法:
上递减;①加法:![]() ②减法:
②减法:![]() ③数乘:
③数乘:![]() ④
④![]() ⑤
⑤![]() .
.

练习册系列答案
相关题目
